一、选择题
(1)分析 从函数f(x)的无定义点入手寻找它的无穷间断点.
精解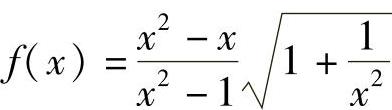 在点x=0,-1,1处无定义.
在点x=0,-1,1处无定义.
由于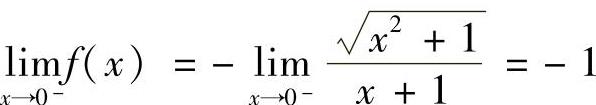 ,
,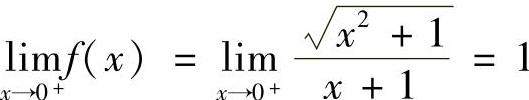 ,
,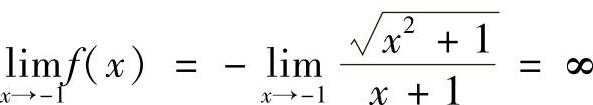 ,
,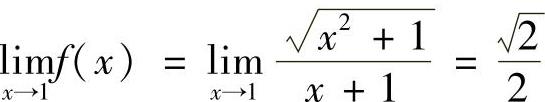 ,
,
所以f(x)只有一个无穷间断点x=-1.
因此本题选(B).
附注 本题的x=0,1都是第一类间断点(前者是跳跃间断点,后者是可去间断点).
(2)分析 将λy1+μy2代入y′+p(x)y=q(x),将λy1-μy2代入y′+p(x)y=0即可算出λ,μ的值.
精解 将λy1+μy2代入y′+p(x)y=q(x)得
λ[y′1+p(x)y1]+μ[y2′+p(x)y2]=q(x). (1)
由于y1,y2都是y′+p(x)y=q(x)的解,即有
y′1+p(x)y1=q(x),y2′+p(x)y2=q(x),
所以,将它们代入式(1),并注意q(x)≠0得
λ+μ=1. (2)
将λy1-μy2代入y′+p(x)y=0,与以上同样计算得
λ-μ=0. (3)
由式(2)、式(3)得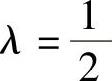 ,
,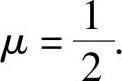
因此本题选(A).
附注 要记住一阶线性微分方程y′+p(x)y=q(x)的通解公式:
其中的每个不定积分只取相应的原函数.
(3)分析 设切点的横坐标为x0,按题设建立关于a,x0的方程,解方程即得a的值.
精解 设切点的横坐标为x0,则有方程
即 
将式(2)改写成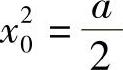 与式(1)比较,并注意a≠0得
与式(1)比较,并注意a≠0得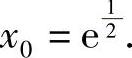 于是
于是
a=2x20=2e.
因此本题选(C).
附注 在未给出切点的情况下,要计算曲线的切线方程或两曲线相切问题时,总是先求出切点坐标.
(4)分析 所给的反常积分是无界函数的反常积分,有瑕点x=1和可能瑕点x=0.于是应分别考虑
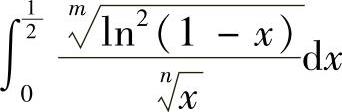 和
和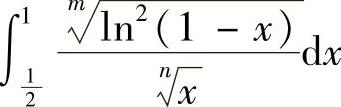 (注意:被积函数在积分区间上是非负的).
(注意:被积函数在积分区间上是非负的).
精解 对于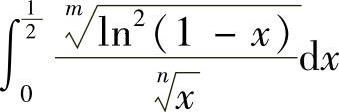 ,当
,当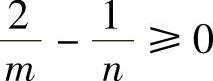 时,
时,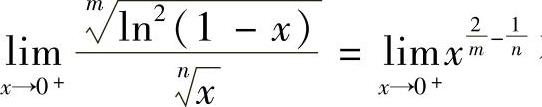 存在,所以此时x=0不是瑕点,即
存在,所以此时x=0不是瑕点,即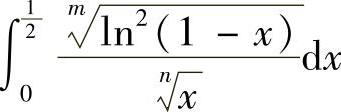 是定积分,可以理解成收敛的反常积分;当
是定积分,可以理解成收敛的反常积分;当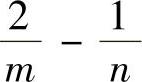
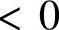 时,x=0是瑕点,此时有
时,x=0是瑕点,此时有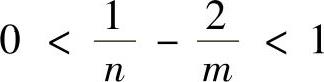 (对任意正整数m,n,都有
(对任意正整数m,n,都有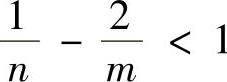 ),且
),且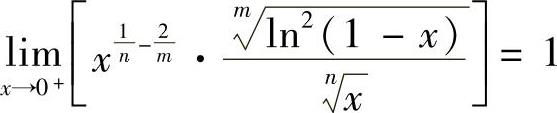 ,所以此时该反常积分收敛.由上可知,对任意正整数m,n,
,所以此时该反常积分收敛.由上可知,对任意正整数m,n,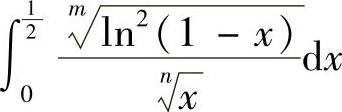 收敛.
收敛.
对于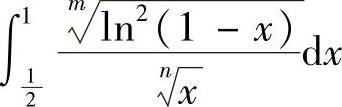 ,由于对任意正整数m,n都有
,由于对任意正整数m,n都有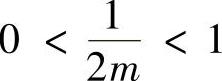 ,且
,且
即对于任意正整数m,n,该反常积分收敛.
因此本题选(D).
附注 应记住无界函数反常积分收敛性的判别法则:
设函数f(x)在(a,b]上连续,且f(x)≥0,但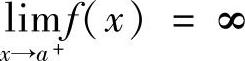 ,如果存在常数0<q<1,使得
,如果存在常数0<q<1,使得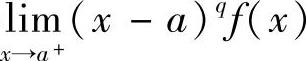 存在,则反常积分
存在,则反常积分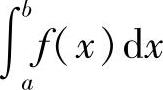 收敛;如果
收敛;如果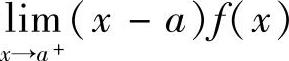 为正数或无穷大,则反常积分
为正数或无穷大,则反常积分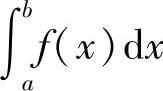 发散.
发散.
(5)分析 为计算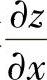 ,
,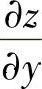 ,从计算所给方程两边的全微分入手.
,从计算所给方程两边的全微分入手.
精解 对所给方程两边求全微分得
即 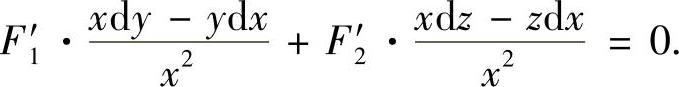
整理后得
所以
从而
因此本题选(B).
附注 要同时计算二元复合函数或隐函数的两个偏导数时,可从计算全微分入手.
(6)分析 利用连续函数的积分和式的极限判定正确选项.
精解
因此本题选(D).
附注 设函数f(x)在[a,b]上连续,则有
(7)分析 利用“当向量组Ⅰ可由向量组Ⅱ线性表示时,r(Ⅰ)≤r(Ⅱ)”的结论即可.
精解 先考察选项(A).
当α1,α2,…,αr线性无关时,由α1,α2,…,αr可由β1,β2,…,βs线性表示得
r=r(α1,α2,…,αr)≤r(β1,β2,…,βs)≤s,
即r≤s.
因此本题选(A).
附注 (i)应记住分析中所述的结论,它在许多场合下是有用的.
(ii)本题也可以按以下定理直接选得正确选项:
设向量组α1,α2,…,αr可由向量组β1,β2,…,βs线性表示,如果向量组α1,α2,…,αr线性无关,则r≤s.
(8)分析 实对称矩阵A可相似对角化,从而只要根据题设条件确定A的特征值即可.
精解 由A是4阶实对称矩阵知A可相似对角化,即
其中λ1,λ2,λ3,λ4是A的特征值.由A满足A2+A=O知这些特征值是方程λ2+λ=0的根,于是λ1,λ2,λ3,λ4为0或-1.由于r(A)=3,所以这些特征值中有且仅有一个为0,其余均为-1.
因此本题选(D).
附注 应记住以下两个结论:
(i)实对称矩阵不仅可相似对角化,而且可正交相似对角化与合同对角化.
(ii)当n阶矩阵A满足f(A)=O(其中f(A)=a0Am+a1Am-1+a2Am-2+…+amEn,En是n阶单位矩阵)时,A的特征值只可能是方程f(λ)=a0λm+a1λm-1+a2λm-2+…+am=0的根.
二、填空题
(9)分析 先算出所给微分方程的特征方程之根,然后按公式写出通解.
精解 所给的三阶常系数齐次线性微分方程的特征方程
r3 -2r2+r-2=0,即 (r-2)(r2+1)=0
有根r=2,i,-i.从而所求的通解为
y=C1e2x+C2cosx+C3sinx (C1,C2,C3是任意常数).
附注 应记住二、三阶常系数齐次线性微分方程的通解与其特征方程之根的对应关系.
(10)分析 从计算所给曲线的铅直渐近线与非铅直渐近线入手.
精解 所给曲线无铅直渐近线.下面计算它的非铅直渐近线.
由于 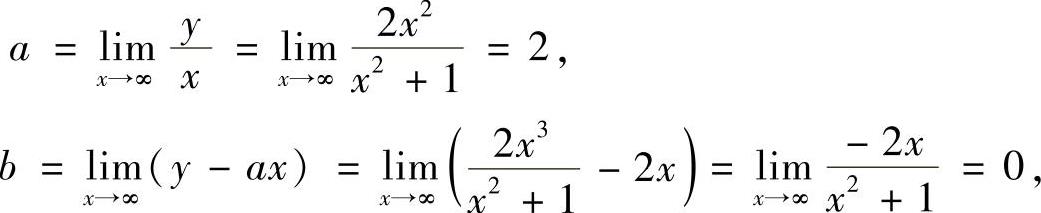
所以,所给曲线有非铅直渐近线y=2x.
综上所述,所给曲线仅有渐近线y=2x.
附注 在计算曲线y=f(x)的非铅直渐近线时,如果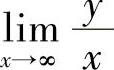 不存在,或者虽然
不存在,或者虽然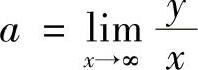 存在,但
存在,但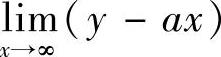 不存在,则应计算
不存在,则应计算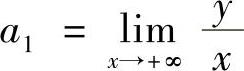 和
和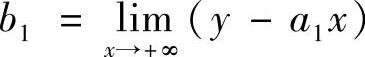 ,也应计算
,也应计算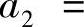
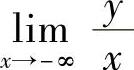 和
和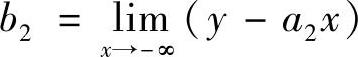 ,才能最后确定曲线y=f(x)的非铅直渐近线.
,才能最后确定曲线y=f(x)的非铅直渐近线.
(11)分析 利用函数y=ln(1-2x)的带佩亚诺型余项的n阶麦克劳林公式计算y(n)(0).
精解 由于函数y=ln(1-2x)的带佩亚诺型余项的n阶麦克劳林公式为
所以, 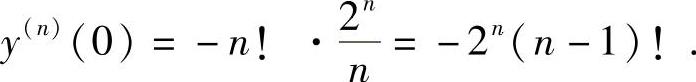
附注 (i)设函数y=f(x)的n阶带佩亚诺型余项的麦克劳林公式为
f(x)=a0+a1x+a2x2+…+anxn+o(xn),
则 f(n)(0)=n!·an.
利用上述公式是快捷算得f(n)(0)的一种方法.
(ii)本题也可按ln(1+ax)的n阶导数公式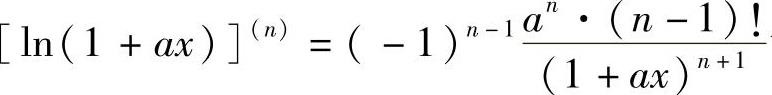 计算:根据这个公式
计算:根据这个公式
所以 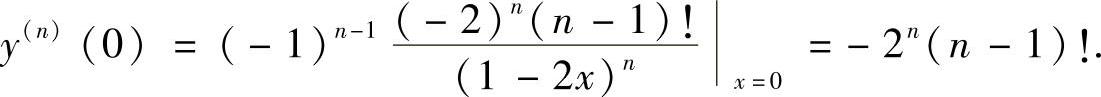
(12)分析 利用极坐标系中曲线弧长公式计算所给曲线r=eθ(0≤θ≤π)的弧长.
精解 曲线r=eθ(0≤θ≤π)的弧长
附注 应记住平面曲线弧长计算公式:
(i)设曲线由参数方程表示: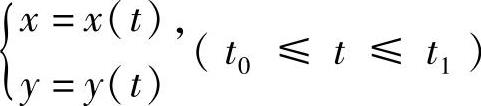 ,则它的弧长
,则它的弧长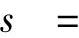
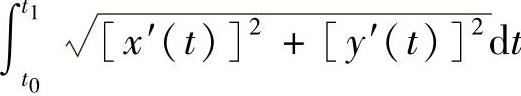 ;
;
(ii)设曲线由极坐标方程表示:r=r(θ)(θ0≤θ≤θ1),则它的弧长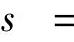
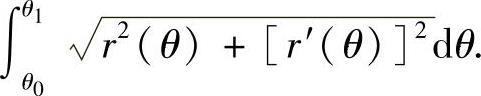
(13)分析 先写出对角线长x关于l,w的函数,然后由复合函数求导算出对角线的增加速率.
精解 由题设知长方形对角线长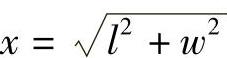 ,其中
,其中
于是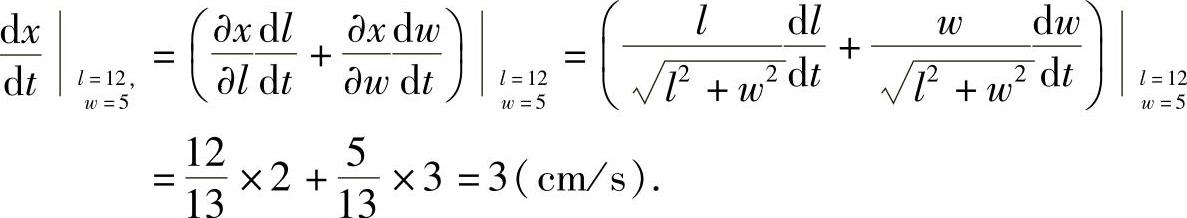
附注 这是一道很简单的题,在一般的教科书中均能见到.
(14)分析 利用矩阵运算,写出用A-1+B表示的A+B-1即可.
精解 由于A+B-1=A(E+A-1B-1)(E是三阶单位矩阵)
=A(B+A-1)B-1=A(A-1+B)B-1,所以,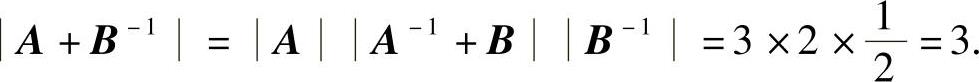
附注 关于矩阵的行列式的以下结论应记住:
设A,B都是n阶矩阵,λ是常数,则
三、解答题
(15)分析 对积分上限函数求导,算出f(x)的所有驻点,然后列表确定f(x)的单调区间与极值.
精解f(x)的定义域为(-∞,+∞),在其上f(x)可导,且由
得 
由此得到f(x)的驻点为-1,0,1.据此列表如下:
由表可知,f(x)的单调减少区间为(-∞,-1]和[0,1],单调增加区间为[-1,0]和[1,+∞),f(x)的极小值为f(-1)=f(1)=0,极大值为(https://www.xing528.com)
附注 要计算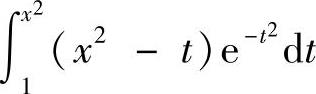 的导数,必须先将x从被积函数中移走,故需将
的导数,必须先将x从被积函数中移走,故需将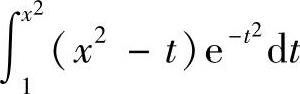 改写成
改写成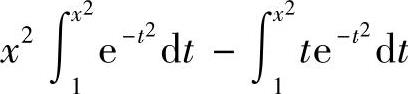 再求导数.
再求导数.
本题是综合题,有关内容与计算方法见提高篇05,06.
(16)分析 (Ⅰ)由于两个定积分的积分区间相同,所以只要比较在(0,1)内[ln(1+t)]n与tn(n=1,2,…)的大小即可.
(Ⅱ)利用(Ⅰ)的结论和数列极限存在准则Ⅰ,计算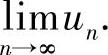
精解 (Ⅰ)由于对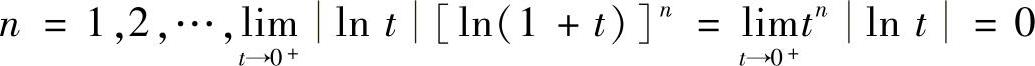 ,即t=0不是瑕点,所以只要比较这两个函数在(0,1)内的大小,即只要比较[ln(1+t)]n与tn在(0,1)内的大小即可.
,即t=0不是瑕点,所以只要比较这两个函数在(0,1)内的大小,即只要比较[ln(1+t)]n与tn在(0,1)内的大小即可.
当0<t<1时,0<ln(1+t)<t,所以对n=1,2,…有
[ln(1+t)]n<tn,
于是有 |lnt|[ln(1+t)]n<tn|lnt|.
从而对n=1,2,…有
(Ⅱ)由(Ⅰ)的证明知,对n=1,2,…有
其中,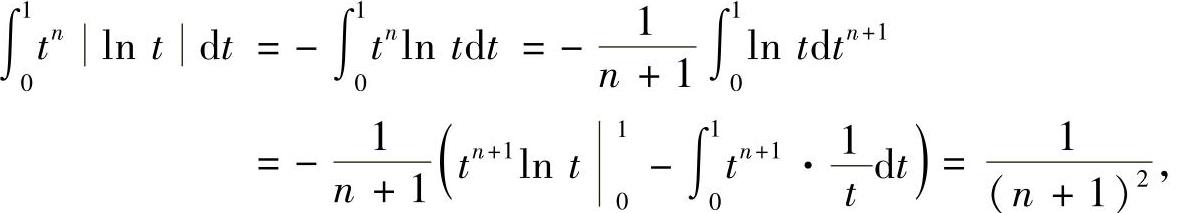
所以有 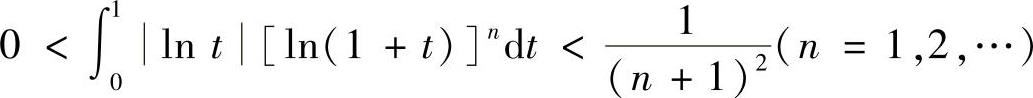 ,且
,且
于是,由数列极限存在准则Ⅰ得
附注 本题(Ⅱ)也可以如下那样快捷证明:
由于对n=1,2,…有
并且 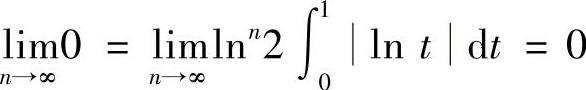 (由于
(由于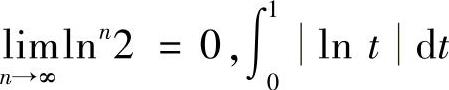 是收敛的反常积分),所以,由数列极限存在准则Ⅰ,知
是收敛的反常积分),所以,由数列极限存在准则Ⅰ,知
本题是综合题,有关内容及方法见提高篇02.
(17)分析 先由对参数方程确定的函数求二阶导数的方法算出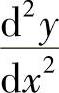 ,再由此得到ψ(t)的微分方程.解此方程即得函数ψ(t).
,再由此得到ψ(t)的微分方程.解此方程即得函数ψ(t).
精解 由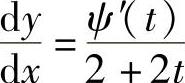 得
得
将它代入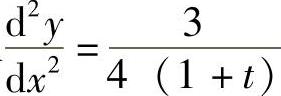 得
得
化简得 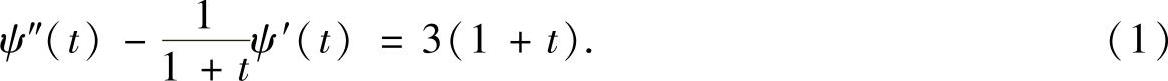
令u=ψ′(t),则式(1)成为
它的通解为
将u(1)=ψ′(1)=6代入式(2)得
C1 =0.
将它代入式(2)得
u=3(1+t)t,即ψ′(t)=3t+3t2,
所以, 
将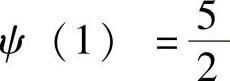 代入式(3)得
代入式(3)得
C2 =0.
将它代入式(3)得
附注ψ(t)满足的二阶线性微分方程(1)不是常系数的,但可以通过自变量t的变量代换转化成二阶常系数线性方程,具体如下:
令1+t=es,则
将它们代入式(1)得
即 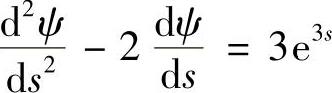 (二阶常系数线性微分方程).
(二阶常系数线性微分方程).
本题是综合题,其有关内容和方法见提高篇03,14.
(18)分析 建立坐标系,算出贮油罐中油的纵截面的面积,记为A,则油的质量为
M=Alρ.
精解 建立坐标系如图B-10-1所示,则椭圆方程为
于是,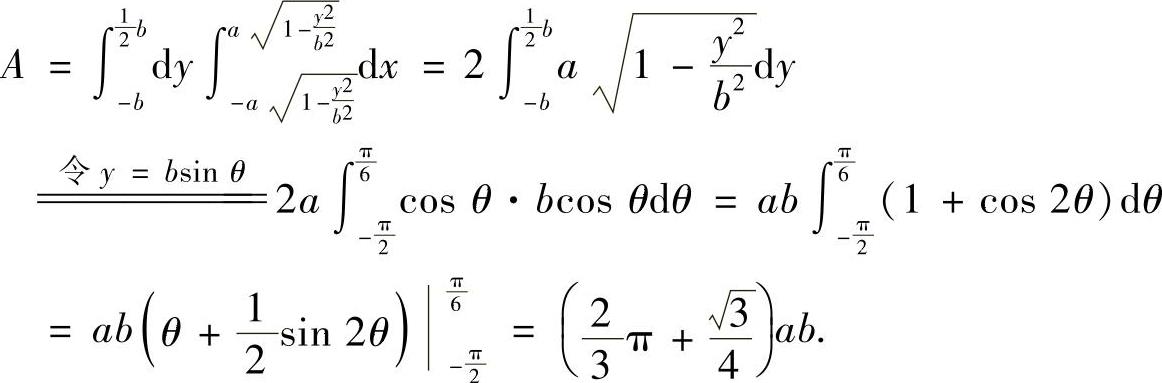
从而贮油罐中油的质量为
图 B-10-1
附注 如果贮油罐是椭球形,即其表面方程为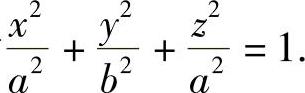 将该贮油罐按y轴朝上地放置于地上,其中贮油的截面同题中图B-10-1阴影部分.那么此时油的质量M1计算如下:
将该贮油罐按y轴朝上地放置于地上,其中贮油的截面同题中图B-10-1阴影部分.那么此时油的质量M1计算如下:
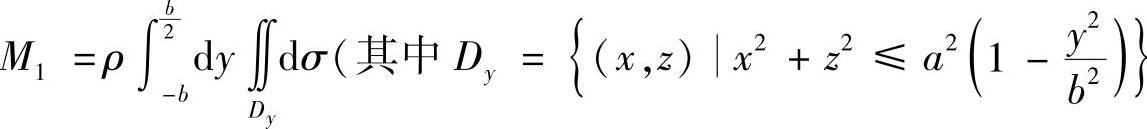 是贮油罐的纵坐标为y的截面)
是贮油罐的纵坐标为y的截面)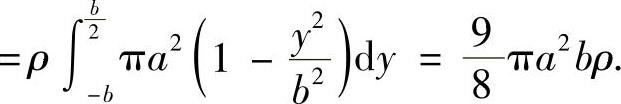
(19)分析 将u关于x,y的二阶偏导数用关于ξ,η的二阶偏导数表示后代入
然后与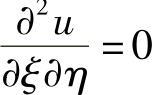 比较即得a,b的值.
比较即得a,b的值.
精解 由于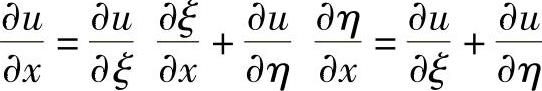 ,
,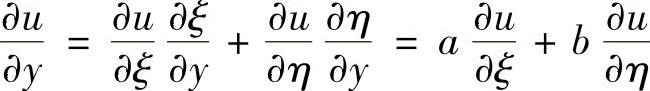 ,
,
所以,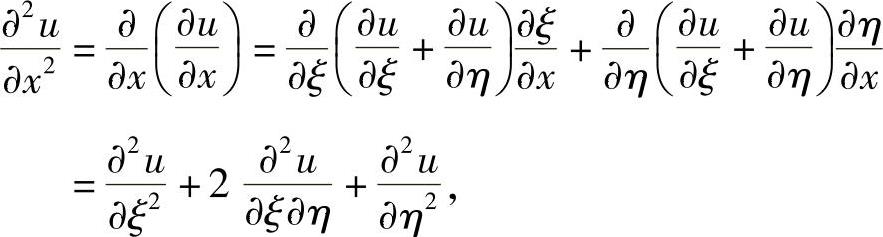
将它们代入式(1)得
化简后得
要使上式成为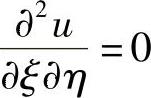 ,a,b必须满足
,a,b必须满足
由式(2)、式(3)得a,b可为-2或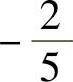 ,组合成
,组合成
显然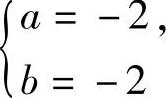 与
与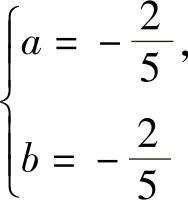 都不满足式(4),因此所求的
都不满足式(4),因此所求的
a=-2,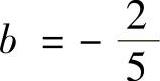 ,或者
,或者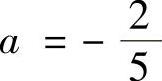 ,b=-2.
,b=-2.
附注 (i)应熟练掌握二元复合函数的一、二阶偏导数的计算方法.
(ii)本题可用以下方法快捷计算:
由于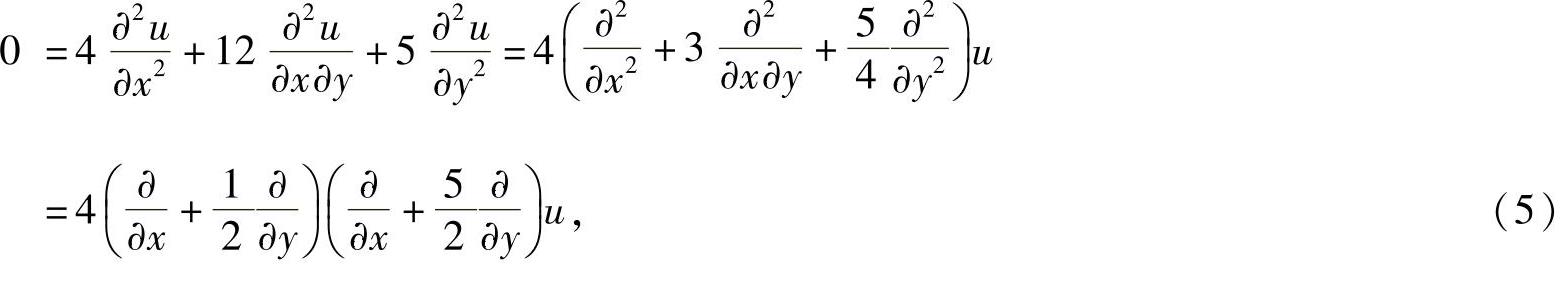
其中,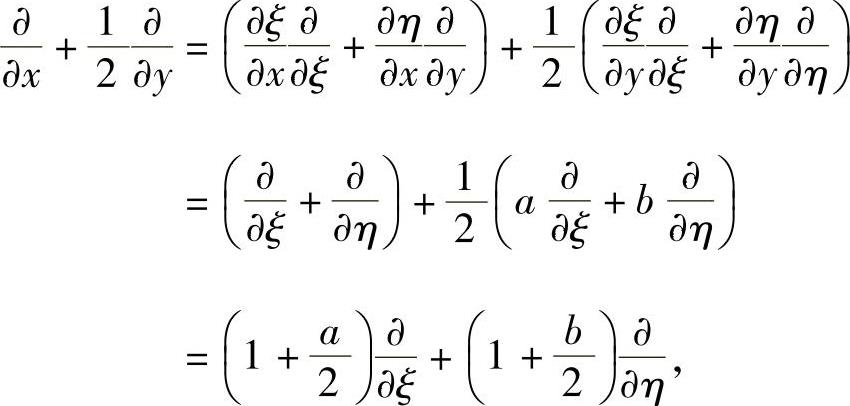
同理 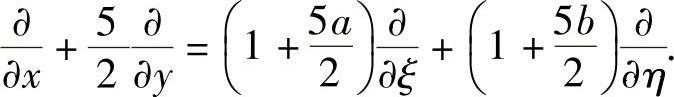
将它们代入式(5)右边得
要使上式成为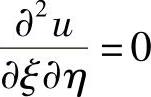 ,a,b必须满足
,a,b必须满足
与题解中同样可得a=-2,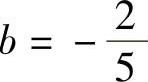 ,或者
,或者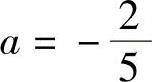 ,b=-2.
,b=-2.
(20)分析 将所给的二重积分转换成直角坐标系下的二重积分后计算.
精解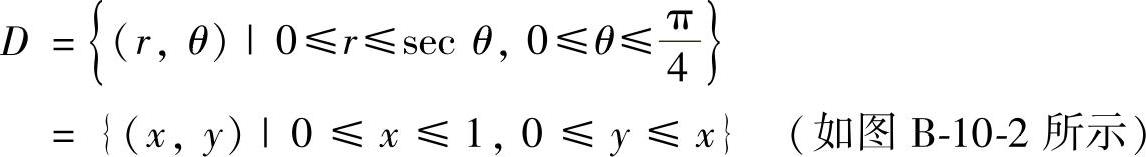
所以,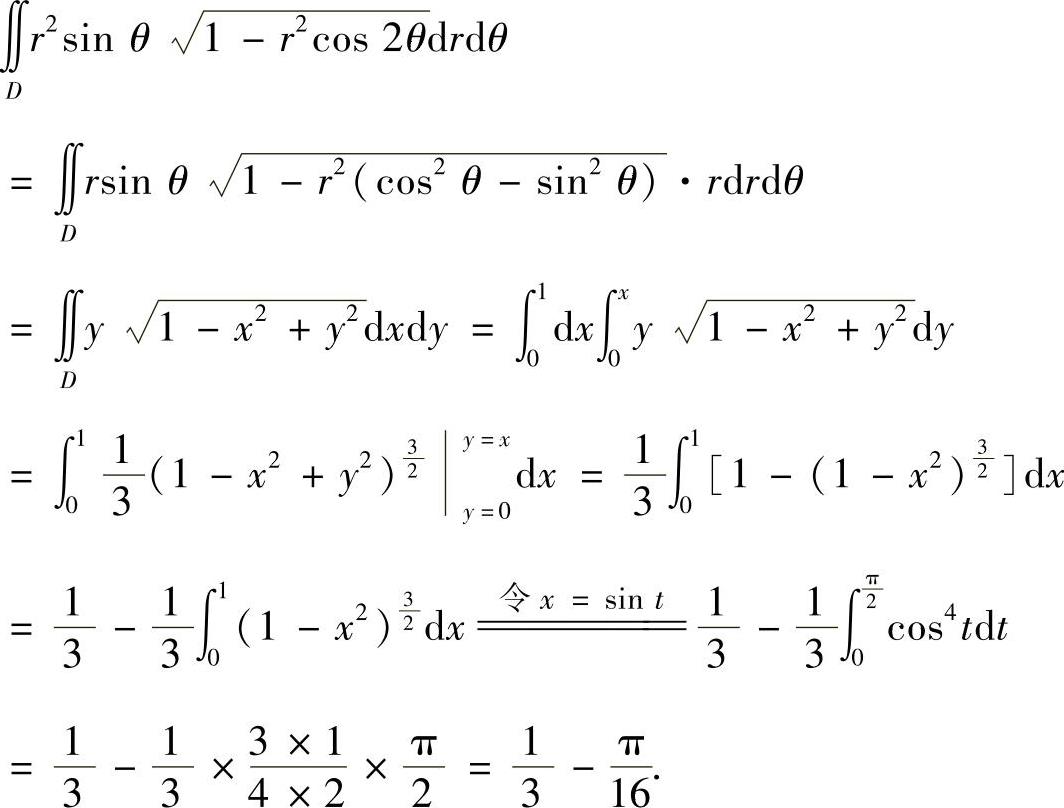
图 B-10-2
附注 本题的二重积分,直接用极坐标计算是比较复杂的,因此将它转化为直角坐标系中的二重积分计算.在题解中应用了以下公式:对n=2,3,4,…,
应熟练掌握直角坐标系下的二重积分与极坐标系下的二重积分之间的相互转换.
(21)分析 欲证的等式即为
[f′(ξ)-ξ2]+[f′(η)-η2]=0,
因此,作辅助函数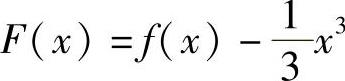 ,分别对它在
,分别对它在 与
与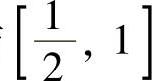 上应用拉格朗日中值定理.
上应用拉格朗日中值定理.
精解 记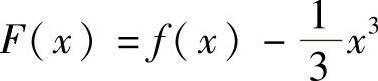 (即f′(x)-x2的一个原函数),则F(x)在
(即f′(x)-x2的一个原函数),则F(x)在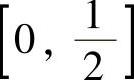 和
和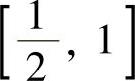 上都满足拉格朗日中值定理条件,所以存在
上都满足拉格朗日中值定理条件,所以存在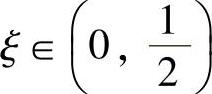 和
和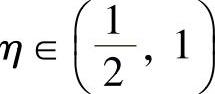 ,使得
,使得
以上两式相加得
2[F(1)-F(0)]=f′(ξ)+f′(η)-ξ2-η2. (1)
由于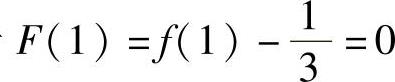 ,
,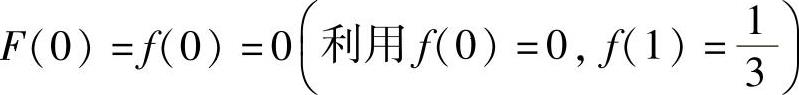 ,所以将它们代入式(1)得
,所以将它们代入式(1)得
f′(ξ)+f′(η)=ξ2+η2.
附注 由于不能确定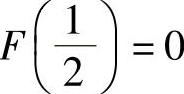 是否成立,所以在
是否成立,所以在 上必须应用拉格朗日中值定理,而不能用罗尔定理.对
上必须应用拉格朗日中值定理,而不能用罗尔定理.对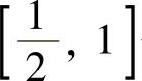 也有相同说法.
也有相同说法.
本题获证的关键是作辅助函数F(x),有关内容与方法见提高篇04.
(22)分析 (Ⅰ)由Ax=b有两个不同解知r(A┊b)=r(A)<3,由此可以算出λ,a.
(Ⅱ)将(Ⅰ)算得的λ,a代入Ax=b,计算它的通解.
精解 (Ⅰ)由于Ax=b有两个不同解知
r(A┊b)=r(A)<3.
对(A┊b)施行初等行变换:
由此可知,λ,a必须满足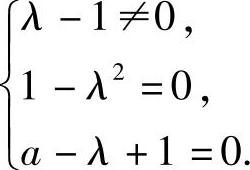 即λ=-1,a=-2.
即λ=-1,a=-2.
(Ⅱ)当λ=-1,a=-2时,Ax=b的增广矩阵为
所以,Ax=b与方程组
同解,式(1)对应的齐次线性方程组有基础解系(1,0,1)T.此外,式(1)有特解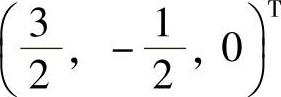 ,所以,式(1)即Ax=b的通解为
,所以,式(1)即Ax=b的通解为
附注n元非齐次线性方程组Ax=b有唯一解的充分必要条件是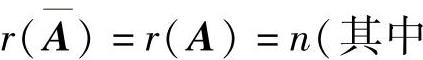
 ,有无穷多解的充分必要条件是
,有无穷多解的充分必要条件是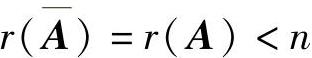 ,无解的充分必要条件是
,无解的充分必要条件是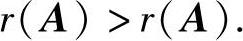
要熟练掌握求解线性方程组的方法,本题的有关内容与方法见提高篇16.
(23)分析 设A的对应特征向量(1,2,1)T的特征值为λ1,由此建立方程组求得a及λ1.然后将算得的a代入A,算出A的其余特征值及对应的特征向量,确定正交矩阵Q.
精解 由题设可知,正交矩阵Q的第1列应是实对称矩阵A的特征向量,所以A有特征向量α1=(1,2,1)T,设它对应的特征值为λ1,则(λ1E-A)α1=0(其中E是3阶单位矩阵),即
由此得方程组
解此方程组得a=-1,λ1=2.
将a=-1代入A得
由于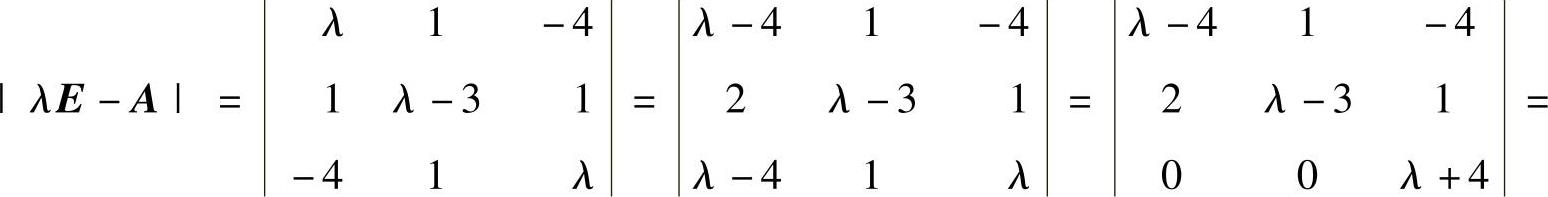
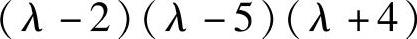 ,所以A有特征值λ1=2,λ2=5,λ3=-4.
,所以A有特征值λ1=2,λ2=5,λ3=-4.
设对应λ2=5的特征向量为x=(x1,x2,x3)T,则x满足
由于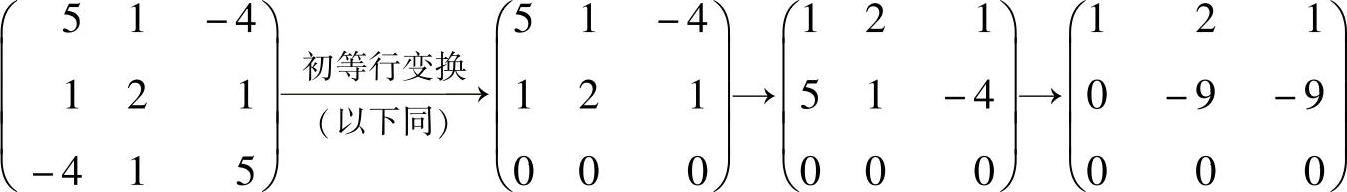
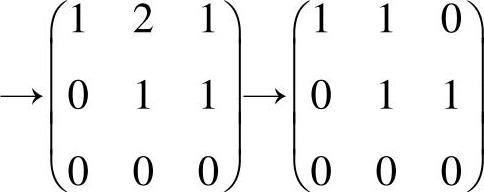 ,
,
所以方程组(1)与
同解,从而可取x为α2=(-1,1,-1)T.
设对应λ3=-4的特征向量为y=(y1,y2,y3)T,则由A是实对称矩阵知y与α1,α2,正交,即
所以y可取α3=(-1,0,1)T.
显然α1,α2,α3两两正交,现将它们单位化得
所以 (正交矩阵),它使
(正交矩阵),它使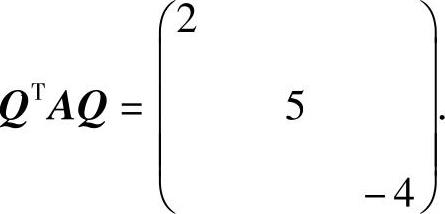
附注 本题是综合题,其有关的计算方法见提高篇18.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




