2014年考研数学真题精解及热点问题

一、选择题

（1）分析 先寻找ln^α（1+2x）与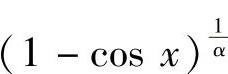在x→0⁺时的等价无穷小，然后由题设即可确定α的取值范围.

精解 由于ln^α（1+2x）在x→0+时是无穷小，所以α＞0.从而有

于是由题知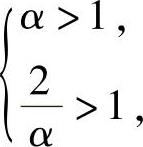即α∈（1，2）.

因此本题选（B）.

附注 首先确定α＞0是需要的，这是因为在不知α＞0时，不能有式（1）.

（2）分析 从计算非铅直渐近线入手.

精解 对选项（C），由于

所以，曲线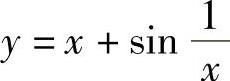有渐近线y=x.

因此本题选（C）.

附注 对于曲线y=y（x），如果极限与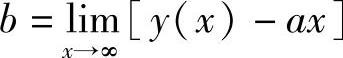都存在，则该曲线有非铅直渐近线y=ax+b.

（3）分析 对f（x）在[0，x]与[x，1]（x∈（0，1））上应用拉格朗日中值定理证明.

精解 当x∈（0，1）时，对f（x）在[0，x]与[x，1]上应用拉格朗日中值定理，于是由

f（x）=f（0）+f′（ξ₁）x （ξ₁∈（0，x）），

f（x）=f（1）+f′（ξ₂）（x-1） （ξ₂∈（x，1））

得 f（x）=f（0）（1-x）+f（1）x+[f′（ξ₁）-f′（ξ₂）]x（1-x）

=g（x）-f″（ξ）（ξ₂-ξ₁）x（1-x） （ξ∈（ξ₁，ξ₂）⊂（0，1））.

所以，当f″（x）≥0（x∈（0，1））时，有f（x）≤g（x）（x∈（0，1））.此外f（0）=g（0），f（1）=g（1），故有，f（x）≤g（x）（x∈[0，1]）.

因此本题选D.

附注 当f″（x）＞0（x∈[0，1]）时，有f（x）≤g（x）（x∈[0，1]），其中仅在点x=0，1处取等号.当f″（x）≥0（x∈[0，1]）时，有f（x）≤g（x）（x∈[0，1]），但是取等号处不限于点x=0与点x=1.

（4）分析 先算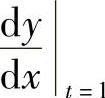与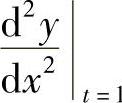，然后用公式计算曲线在对应于t=1的点处的曲率半径.

精解 由于，，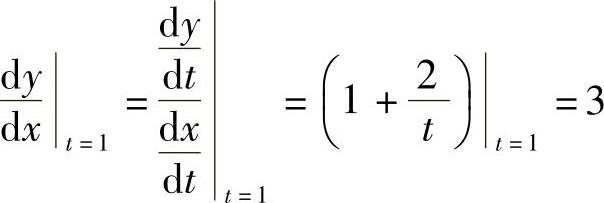

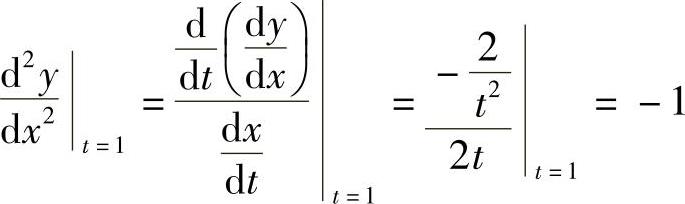所以，所求的曲率半径为

因此本题选（C）.

附注 曲线y=y（x）在点（x₀，y（x₀））处的曲率为

所以，在该点处曲线的曲率半径为

（5）分析 先算出ξ²的表达式，然后计算极限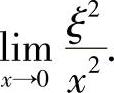

精解 由f（x）=f′（ξ）x，即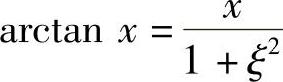得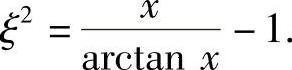

于是有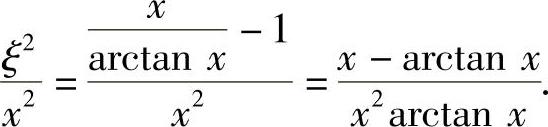

由此得到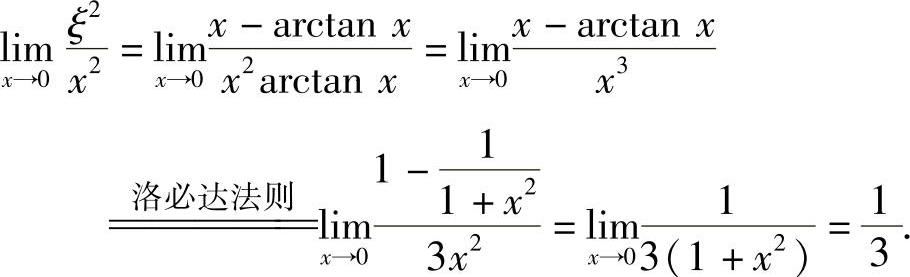

因此本题选（D）.

附注 题中的f（x）=f′（ξ）x是f（x）在[0，x]（或[x，0]）上应用拉格朗日中值定理得到的，其中ξ∈（0，x）（或（x，0）），是其中值.

（6）分析 用反证法证明u（x，y）在D的内部取不到最大值和最小值.

精解 设函数u（x，y）在点（x₀，y₀）（其中（x₀，y₀）位于D的内部）取到最大值，则u（x₀，y₀）是极大值，故有

但由题设知

以上矛盾表明u（x，y）在D的内部取不到最大值.同理可知，u（x，y）在D的内部也取不到最小值.但连续函数u（x，y）在有界闭区域D上必取到最大值与最小值，所以u（x，y）的最大值与最小值都在D的边界上取到.

因此本题选（A）.

附注 当u（x，y）（具有连续的二阶偏导数）在点（x₀，y₀）处取到极值时，未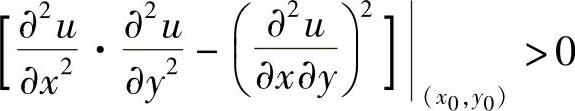必有，但必有

（7）分析 按第1行展开即可.

精解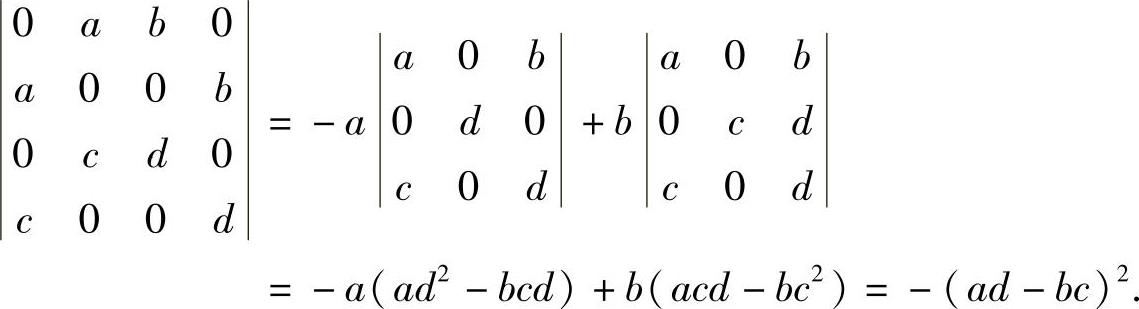

因此本题选（B）.

附注 本题可按任一行（列）展开计算.

（8）分析 按向量组线性无关的定义进行推理.

精解 设α₁，α₂，α₃线性无关，则对常数λ₁，λ₂有

λ₁（α₁+kα₃）+λ₂（α₂+lα₃）=0，即λ₁α₁+λ₂α₂+（λ₁k+λ₂l）α₃=0

时，必有λ₁=λ₂=0，由此可知，α₁+kα₃，α₂+lα₃线性无关.

但反之未必成立，例如α₁=（1，0，0）^T，α₂=（0，1，0）^T，α₃=（0，0，0）^T，则α₁+kα₃=α₁，α₂+lα₃=α₂线性无关，但α₁，α₂，α₃却线性相关.

因此本题选（A）.

附注 本题的必要性也可证明如下：

设α₁，α₂，α₃是线性无关的三维列向量组，则由

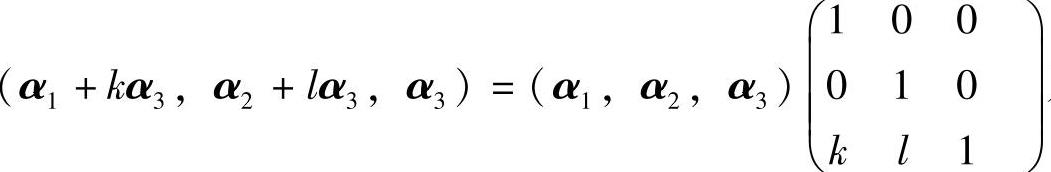及矩阵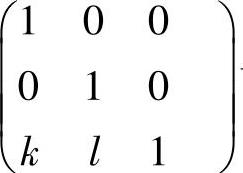可逆知，α₁+kα₃，α₂+lα₃，α₃线性无关，从而α₁+kα₃，α₂+lα₃线性无关.

二、填空题

（9）分析 按收敛反常积分的牛顿-莱布尼茨公式计算.

精解 由于所给的反常积分是收敛的，所以

附注 对收敛的反常积分，也有与定积分类似的牛顿-莱布尼茨公式，以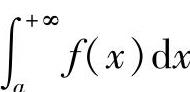为例.设F（x）是f（x）的一个原函数，则

（10）分析 先算出f（x）在[0，2]上的表达式，然后利用f（x）的周期性和奇偶性算出f（7）.

精解 由于f（x）是奇函数，所以f（0）=0.于是

由于f（x）是以4为周期的奇函数，所以

f（7）=f（-1）=-f（1）=1.

附注 写出f（x）在[0，4]（即一个周期）上的表达式.

由x∈[0，2]时，f（x）=x²-2x知，x∈[-2，0）时，f（x）=-x²-2x.

从而当x∈[2，4]时，f（x）=f（x-4）=-（x-4）2-2（x-4）=-x²+6x-8.因此

（11）分析 由所给方程确定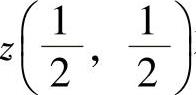存在且为唯一，解出z，然后计算dz，并将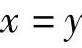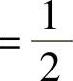，z代入即可.

精解 将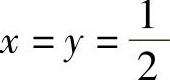带入方程得e^z+z=1，可看出z=0为满足条件的解.把原方程看成三元函数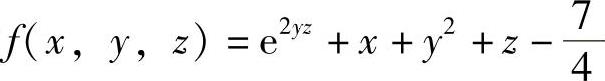，则有f_x=1，f_y=2ze^2yz+2y，f_z=2ye^2yz+1.将z看成x和y的函数，把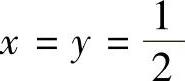代入f_y，f_z则有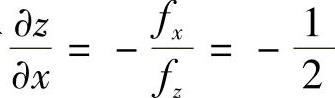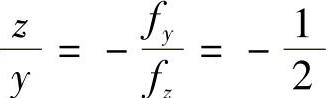，，所以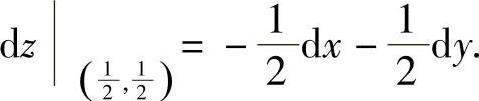

（12）分析 将L的极坐标方程转换成参数方程，然后计算切线的直角坐标方程.

精解 由于L的方程可以写成参数为θ的方程

且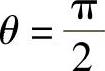对应的x=0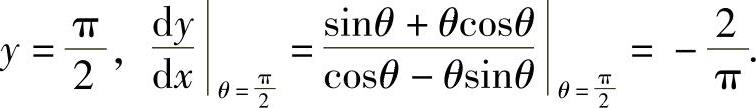，所以，所求的切线的直角坐

标方程为

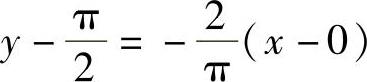，即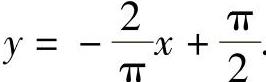

附注 当曲线的极坐标方程为r=r（θ）时，它的参数方程为

（13）分析 由于质心坐标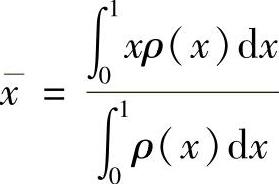，所以只要算出上式中的两个定积分即可.

精解 由于，，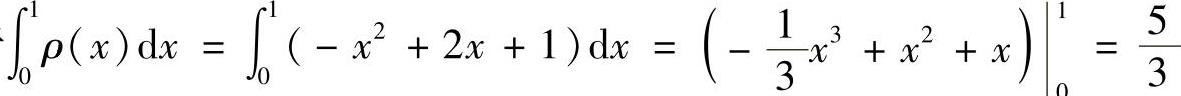

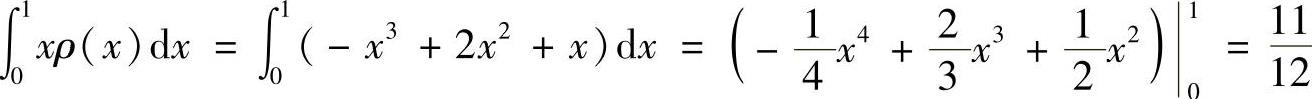所以，质心坐标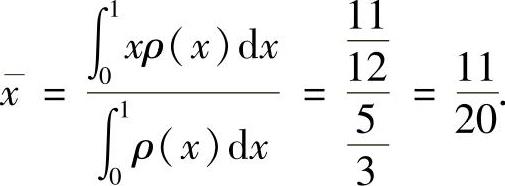

附注 当区间[a，b]上有质量分布，其密度为ρ（x），则质心坐标

当平面区域D上有质量分布，其密度为ρ（x，y），则质心坐标

对于空间区域Ω也有相应的质心坐标计算公式.

（14）分析 用配平方的方法将f（x₁，x₂，x₃）转换成标准形即可确定a的取值范围.

精解 由于

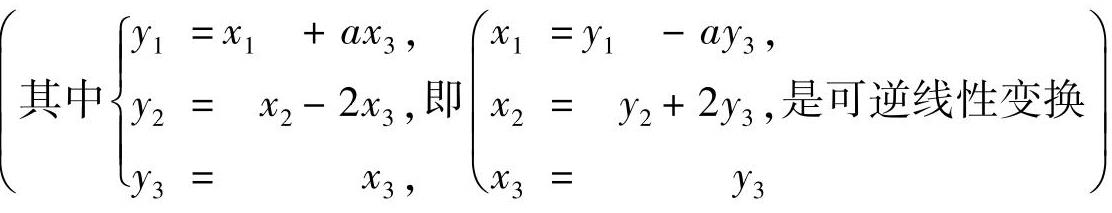，所以f（x₁，x₂，x₃）的负惯性指数为1时，a应满足4-a²≥0，故a的取值范围为[-2，2].

附注 对二次型f（x₁，x₂，x₃）进行可逆线性变换，不改变其矩阵的秩，也不改变其正惯性指数（或负惯性指数）的值.

三、解答题

（15）分析 用洛必达法则计算所给的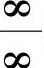型未定式极限.

精解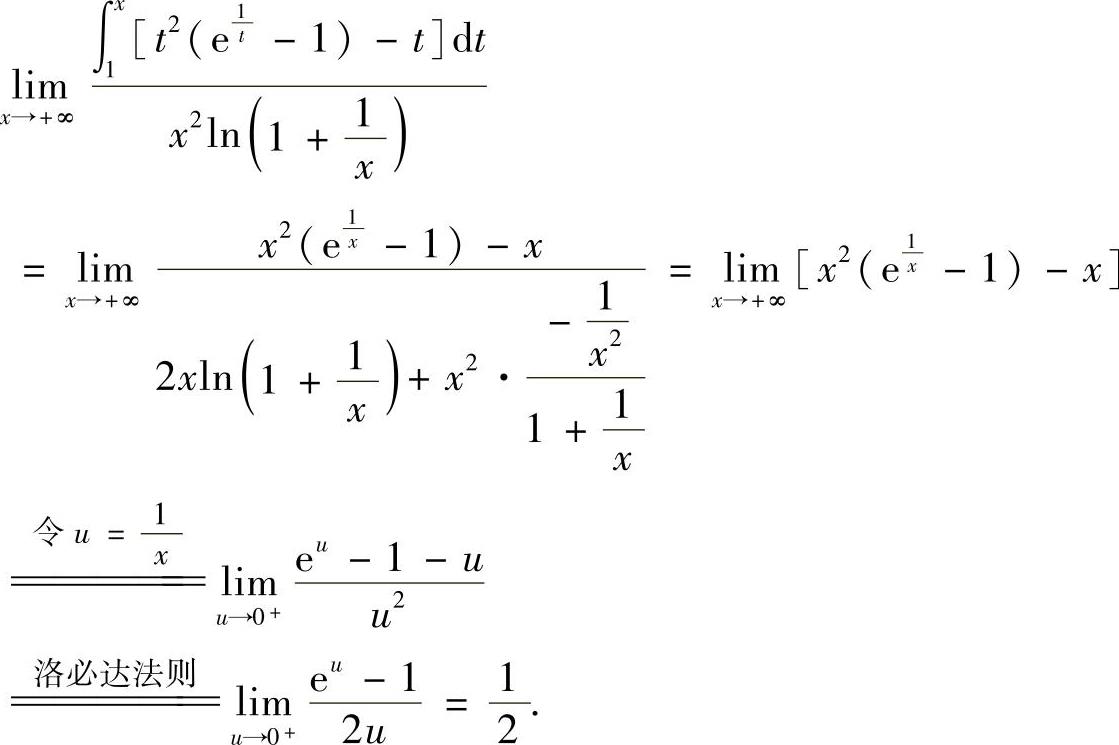

附注 本题也可以用以下方法求解：

本题是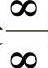型未定式极限计算，在基础篇第二章六及提高篇01中可以找到类似的例题.

（16）分析 由所给微分方程及y（2）=0算出y=y（x）及y′，y″，由此即可算出y（x）的极大值与极小值.(www.xing528.com)

精解 将所给微分方程x²+y²y′=1-y′改写成

（y²+1）dy=（1-x²）dx （1）

即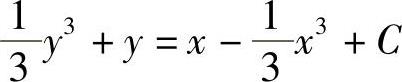，将y（2）=0代入得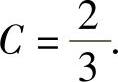所以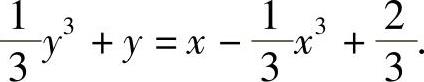

由式（1）得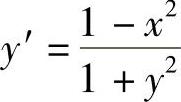.所以y（x）的可能极值点为x=-1，1，显然y（-1）=0，y（1）=1.

由于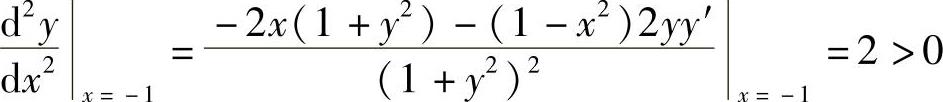，所以y（x）的极小值为y（-1）=0，

由于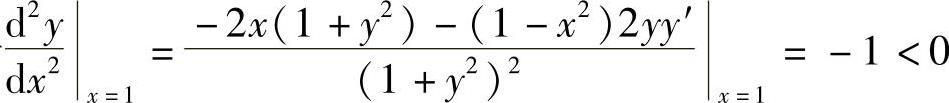，所以y（x）的极大值为y（1）=1.

附注 本题是函数极值计算与微分方程求解的综合题，在提高篇06，013中给出了这类综合题的典型例子.

（17）分析 由于积分区域是角域的一部分，所以用极坐标计算所给的二重积分.

精解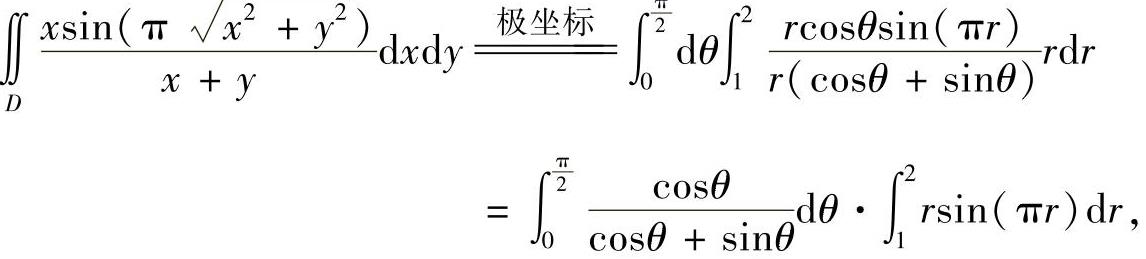

其中，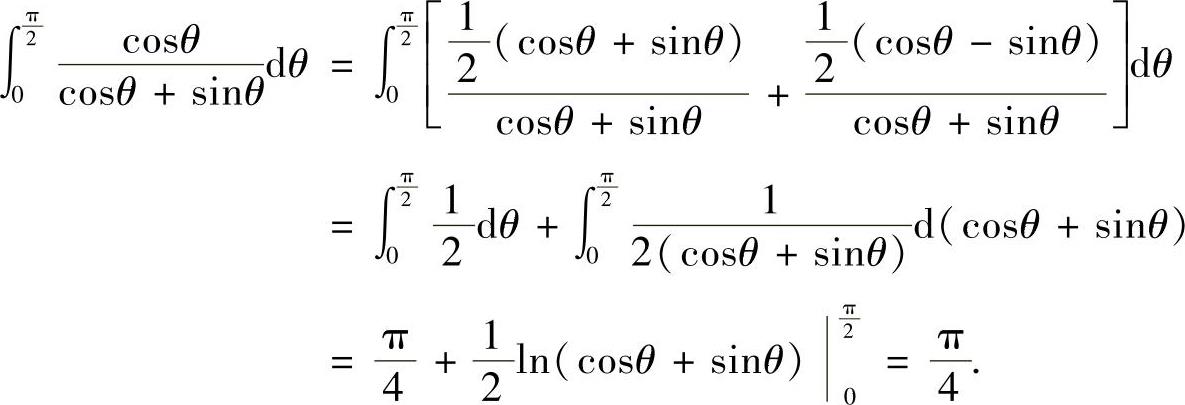

所以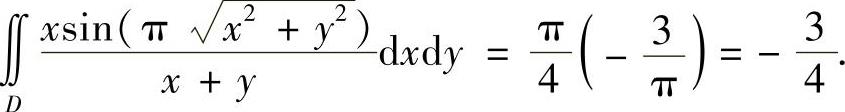

附注 当积分区域D是角域一部分，即D={（r，θ）|r₀≤r（θ）≤r₁，0≤θ₀≤θ≤θ₁≤2π}时，通常用极坐标计算二重积分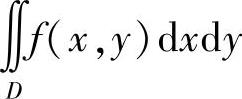（其中f（x，y）在D及其边界上连续）.

在基础篇第三章八及提高篇12中可以找到类似的例题.

（18）分析 先计算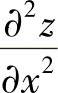与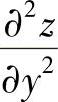，并利用它们满足的等式得到关于f（u）的微分方程，然后求解该微分方程得到f（u）的表达式.

精解 由dz=f′（u）[e^xcosydx+（-e^xsiny）dy]（其中u=e^xcosy）得

所以，，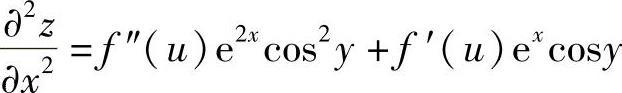

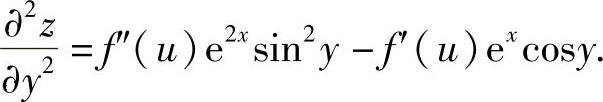
从而由所给等式得

f″（u）e^2x=[4f（u）+u]e^2x，

即 f″（u）-4f（u）=u.（二阶常系数非齐次线性微分方程） （1）

由于f″（u）-4f（u）=0有通解F=C₁e^2x+C₂e^-2x，以及f″（u）-4f（u）=u有特解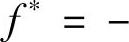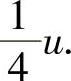所以式（1）的通解为

且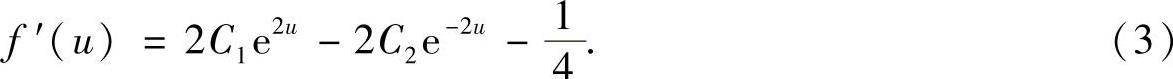

将f（0）=f′（0）=0代入式（2）、式（3）得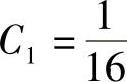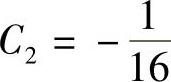，，将它们代入式（2）得

附注 本题是偏导数计算与求解二阶常系数线性微分方程的综合题，应熟练掌握一、二阶偏导数的计算和二阶常系数线性微分方程的解法.

在提高篇14中可以找到与本题十分相似的例题.

（19）分析 （Ⅰ）可由0≤g（x）≤1直接得到.

（Ⅱ）将欲证不等式中的b换成x，然后利用对变上限积分求导数的方法证明.

精解 （Ⅰ）对x∈[a，b]，由0≤g（x）≤1得

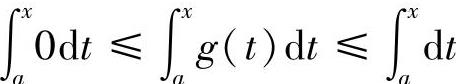，即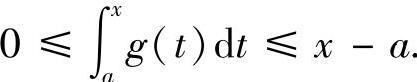

（Ⅱ）将欲证不等式中的b改为x，并记

则F（x）在[a，b]上可导，且

所以，F（b）≤F（a）=0，即

附注 含定积分的不等式的证明方法在基础篇九及提高篇05中有详细叙述，并在其中可以找到与本题相似的例题.

（20）分析 先写f_n（x）的表达式，并由此计算S_n，然后求极限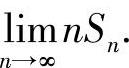

精解 根据函数列的定义得x∈[0，1]时.

依此类推得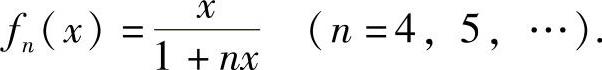

由于f_n（0）=0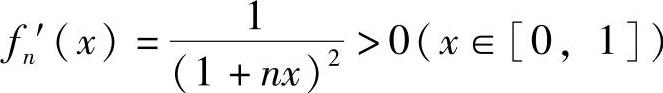，，所以由曲线y=f_n（x），直线x=1及x轴围成的概图如图B.14.1的阴影部分所示.由此得到

图 B.14.1

从而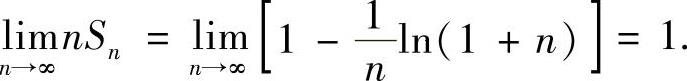

附注 照理对n=1，2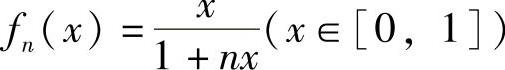，…，需用数学归纳证明.具体如下：

显然n=1，2时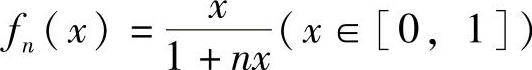，是正确的.现设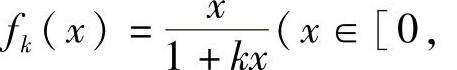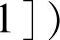，则对x∈[0，1]有

于是，对n=1，2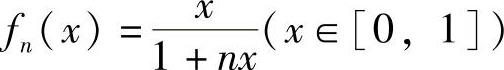，…，正确.

（21）分析 先算出f（x，y）的表达式，画出曲线f（x，y）=0与y轴围成的平面图形，然后按公式计算旋转体体积.

精解 由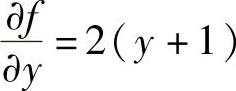得f（x，y）=（y+1）²+φ（x）.于是将

f（y，y）=（y+1）²+φ（y）

与所给的f（y，y）=（y+1）²-（2-y）比较得φ（y）=y-2，从而

f（x，y）=（y+1）²+x-2.

于是由曲线f（x，y）=0与y轴围成的平面图形D如图B.14.2阴影部分所示，于是D绕直线y=-1旋转一周而成的旋转体体积

图 B.14.2

V=D的位于直线v=-1以上部分绕该直线旋转一周而成的旋转体体积

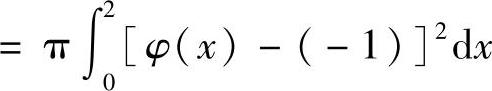（其中y=φ（x）是曲线f（x，y）=0位于直线y=一1上方

部分的方程，它满足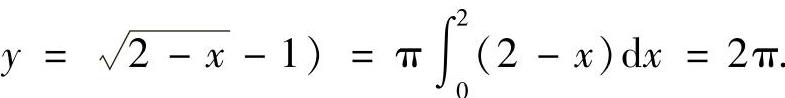

附注 记由曲线y=f₁（x），y=f₂（x）及直线x=a，x=b（其中f₁（x），f₂（x）在[a，b]上连续，且c≤f₁（x）≤f₂（x）（x∈[a，b]）围成的平面区域为D，则D绕x轴旋转一周而成的旋转体体积为

在提高篇10中可以找到与本题类似的例题.

（22）分析 （Ⅰ）对矩阵A施行初等行变换化为阶梯形矩阵，求出方程组Ax=0的一个基础解系.

（Ⅱ）用解矩阵方程方法算出满足AB=E的所有矩阵B.

精解 （Ⅰ）由于

所以方程组Ax=0的一个基础解系为（-1，2，3，1）T.

（Ⅱ）记B=（β₁，β₂，β₃）（其中β₁，β₂，β₃都4维列向量），则AB=E即为三个方程组，，

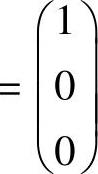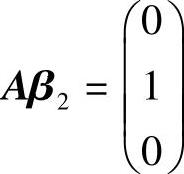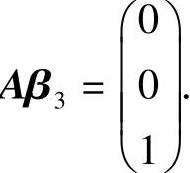
由于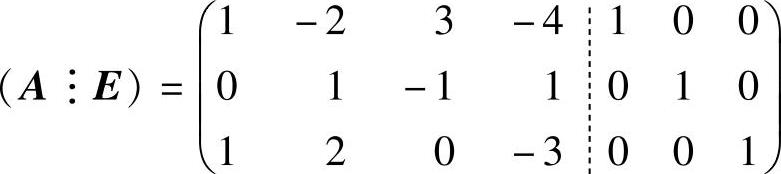

所以，Aβ₁=0的基础解系为（-1，2，3，1）^T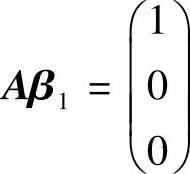，有特解（2，-1，-1，0）T.从而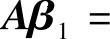的通解为

β₁=c₁（-1，2，3，1）^T+（2，-1，-1，0）^T=（-c₁+2，2c₁-1，3c₁-1，c₁）^T.

同样可得 β₂=（-c₂+6，2c₂-3，3c₂-4，c₂）^T，

β₃=（-c₃-1，2c₃+1，3c₃+1，c₃）^T.

因此满足AB=E的所有矩阵B为

其中c₁，c₂，c₃是任意常数.

附注 本题（Ⅱ）是矩阵方程的求解.

对于矩阵方程 AX=B （∗）

的解法如下：

当A可逆时，X=A^-1B.

当A不可逆时，对式（∗）的增广矩阵（A︙B）施行初等行变换，成为（C︙D）（其中C是阶梯形矩阵，且每个非零行的最靠左边的非零元素都为1），由此可以算出Ax=0的一个基础解系，ξ₁，ξ₂，…，ξ_r，记γ=c₁ξ₁+c₂ξ₂+…+c_rξ_r（其中c₁，c₂，…，c_r是任意常数），也可以算各个方程组Ax=β₁，Ax=β₂，…，Ax=β_l（其中β₁，β₂，…，β_l是B的l个列向量）的特解，记为γ₁，γ₂，…，γ_l，则

X=（γ+γ₁，γ+γ₂，…，γ+γ_l）.

关于矩阵方程的解法在基础篇第六章三中作了详细的叙述，在该节及提高篇16中可以找到与本题十分相似的例题.

（23）分析 只要证明矩阵和矩阵都可相似对角化，且它们具有相同的对角形矩阵即可.

精解 记E是n阶单位矩阵，则由

知，A有特征值λ=n，0（n-1重）.由于A是实对称矩阵，所以A可相似对角化，故

由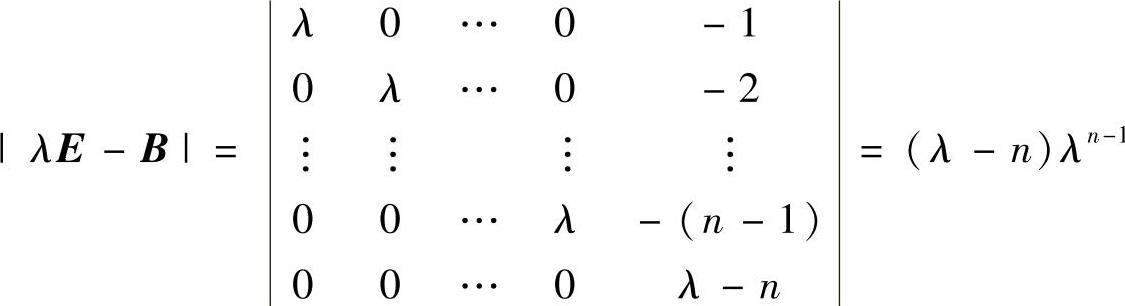

知，B有特征值λ=n，0（n-1重）.

设B的对应λ=n的特征向量为α=（a₁，a₂，…，a_n）^T，则

故可取α=η₁=（1，2，…，n）^T.

设B的对应λ=0的特征向量为β=（b₁，b₂，…，b_n）^T，则

显然b_n=0，b₁，b₂，…，b_n-1可以任取，故取β为

且η₁，η₂，…，η_n线性无关.于是B有n个线性无关的特征向量η₁，η₂，…，η_n，所以B可相似对角化，且

因此A与B相似.

附注 应当注意：当两个n阶矩阵A与B有相同的特征值时，它们未必相似；但是当A与B有相同的特征值，且都有n个线性无关的特征向量时，它们必相似.

本题实际上是n阶矩阵相似对角化的问题，在基础篇第六章七中，详细叙述了n阶矩阵可相似对角化的条件及相似对角化方法.