微型计算机原理数制转换及对照关系十进制转二进制方法

数制即数的表示方式，按进位的方法进行计数称为进位计数制，这也是我们通常使用的数制。数是客观事物的量在人脑中的反应，可以用不同的数制来度量，相同的量用不同的数制来表示将得到不同的结果。在日常生活中使用最多的数制当属“逢十进一”的十进制数，还有一些用于特定领域的特殊进位计数制，如七进制（星期）、十二进制（时间和英制长度）和六十进制（时间和角度）等。而在计算机中，由于具有两种不同稳定状态并能够相互转换的器件比较容易找到，所以只需要两种数字符号的二进制数就理所当然地成为了计算机中最常用的数制。同时，由于二进制数阅读比较困难，与二进制之间转换非常容易的八进制数和十六进制数在计算机中也经常被使用。

一般情况下，一个R进制数：

1）有R个不同的数字符号；

2）逢R进一。

一个R进制数N可以被书写为a_n-1a_n-2…a₁a₀.a_-1a_-2…a_-m，这种写法被称为位置表示法，各个位置上的a_i是R个不同的数字符号之一，R被称为基数。上面的R进制数A可以按权展开为：

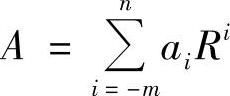
很显然，在位置表示法中，每个数码a_i代表的数值等于该数码乘以一个与所在数位相关的常数Rⁱ，这个常数通常称为位权，或简称权。

1.十进制数

十进制数是我们最常见的数制，它的特点是：

1）有10个不同的数字符号：0、1、2、3、4、5、6、7、8、9；

2）逢10进一。

十进制数的基数为10，即每个位的位权都是其下一个位的10倍。

2.二进制数

二进制数是计算机中最常用的数制，它的特点是：

1）有2个不同的数字符号：0、1；

2）逢2进一。

二进制数的基数为2，即每个位的位权都是其下一个位的2倍。一个二进制数可以用它的按权展开式来表示，例如：

（1100.01）2=1×2³+1×2²+0×2¹+0×2⁰+0×2^-1+1×2^-2=（12.25）₁₀

其中用（）2的形式表示括号中的数为二进制数，其他进制数也可以用类似的方式来表示，例如（）10表示十进制数，（）16表示十六进制数。由于十进制数的使用比较广泛，很多时候十进制数的（）10就不再标注了。

除了这种下标表示法之外，我们还经常使用另外一种计算机领域经常使用的表示不同数制的表示法，即字母后缀法。在字母后缀法里，不带任何字母后缀的数被默认为是十进制数，二进制数则带有一个B字母的后缀（即Binary的首字母），下面介绍的八进制和十六进制则分别以O（Octal）和H（Hexadecimal）为后缀。

除此之外，不同数制的数在一些特定的编程语言中还有一些不同的表示方法（比如在C语言里用0x前缀表示十六进制数等），这里就不一一列举了。

3.十六进制数和八进制数

虽然二进制数对于计算机来讲最自然和易用，但长长的二进制数对于人的阅读和记忆就显得十分烦琐了，为此，在阅读、输入等过程中，人们通常用十六进制数和八进制数来代替二进制数。十六进制和八进制的基数分别为16和8，它们的特点是：

1）十六进制有16个不同的数字符号：0-9和A-F，八进制有8个不同的数字符号：0-7；

2）十六进制逢16进一，八进制逢8进一。

由于2⁴=16、2³=8，所以十六进制数、八进制数和二进制数之间存在着非常简单的对应关系：4位二进制数对应于一位十六进制数，3位二进制数对应于一位八进制数。这种对应关系使得二进制数和八进制数、十六进制数之间的转换非常容易。表2-2给出的就是这三种数制之间的对照关系。

表2-2 三种数制之间的对照关系

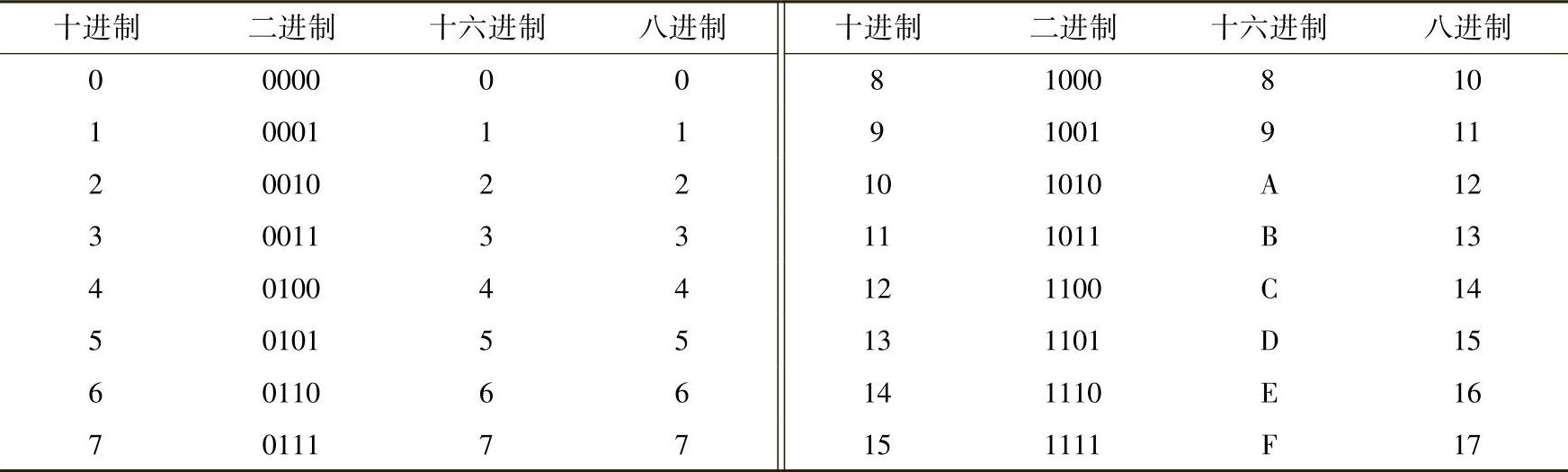
4.各种数制之间的转换

在计算机领域中，通常使用到的数制间转换可以被分为两类：二进制数/八进制数/十六进制数之间的转换，和它们与十进制之间的转换。由于二进制数、八进制数和十六进制数之间存在表2-2中给出的简单的对应关系，简单地进行分组替换就可以达到目的了。比如从二进制数转换为十六进制数，就可以用一位十六进制数代替四位二进制数即可。例如：

（1001010101.01111）₂=（0010 0101 0101.0111 1000）₂=（255.78）16

反之亦然，例如：(www.xing528.com)

（3F8.5A）₁₆=（0011 1111 1000.0101 1010）₂=（1111111000.0101101）₂

二进制数和八进制数之间的转换与之类似，只是一位八进制数对应的是三位二进制数而不是四位而已。

从二进制数/八进制数/十六进制数转换为十进制数可以采用按权展开求和的方式，例如：

（1001010101.01111）2=1×2⁹+0×2⁸+0×2⁷+1×2⁶+0×2⁵+1×2⁴+0×2³+1×2²+0×2¹+1×2⁰+0×2^-1+1×2^-2+1×2^-3+1×2^-4+1×2^-5=512+64+16+4+1+0.25+0.125+0.0625+0.03125=（597.46875）₁₀。

（3F8.5A）16=3×16²+15×16¹+8×16⁰+5×16^-1+10×16^-2=768+240+8+0.3125+0.0390625=（1016.3515625）₁₀。

相反方向的转换，即从十进制数转换为二进制数/八进制数/十六进制数则采用除/乘基取余/整法。其规则如下：对于一个要转换为二进制数/八进制数/十六进制数的十进制数，先分离其整数部分和小数部分，对整数部分采用除基取余法，对小数部分采用乘基取整法。具体来讲，①对于整数部分，每次只取整数商，将余数作为转换结果的一位，重复对整数商除基数，直到商为0为止，将余数按从低位到高位的次序排列起来，就得到了转换结果。②对于小数部分，每次把乘积的整数部分取走作为转换结果的一位，余下部分继续进行乘法运算。对于某些小数，可以乘到积的小数为0，这时转换结果是精确的；而对于某些数永远也不能把小数部分乘到0，这时就只能根据精度要求取一定位数的结果，其转换结果是不精确的。

下面给出两个例子。

①十进制数24.25转换成二进制数：

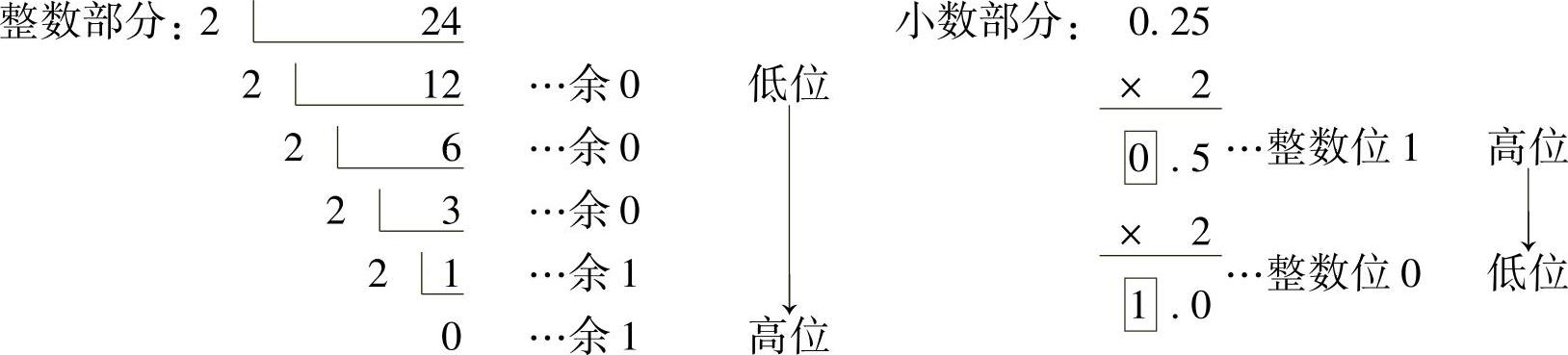
把整数部分和小数部分接起来，得到：（24.25）₁₀=（11000.01）₂。

②十进制数394.625转换成十六进制数：

把整数部分和小数部分接起来，得到：（394.625）₁₀=（18A.A）₁₆。

5.二进制数的运算

二进制数的运算可以分为两类：算术运算和逻辑运算。算术运算的基本规则和十进制数的基本规则是一样的，唯一差别在于二进制数的算术运算逢二进一，借一当二。

加法例子：

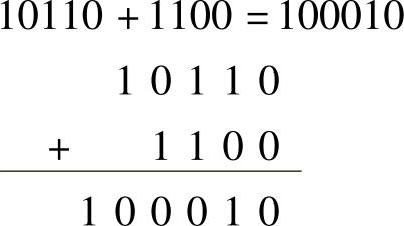
减法例子：

乘法例子：

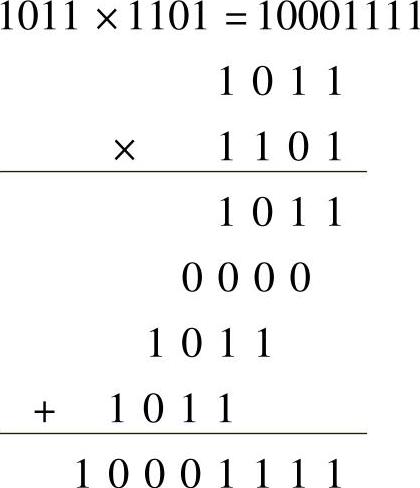
除法例子：

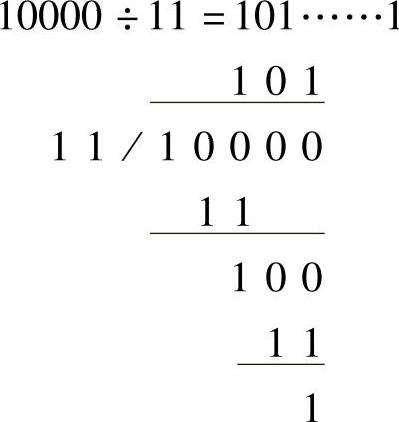
除了算术运算之外，二进制数还可以进行逻辑运算。逻辑运算，又称布尔运算，是计算机中二进制数最基本的运算。常见的逻辑运算有与（AND）、或（OR）、非（NOT）、异或（XOR）等。二进制数的逻辑运算规则如表2-3表示。

表2-3 二进制数的逻辑运算规则

二进制数的逻辑运算由于不涉及到进位借位等问题，运算时只要按位进行运算就可以了。例如：

10011100 AND 10101001=10001000,

10011100 0R 10101001=10111101,

10011100 XOR 10101001=00110101,

NOT 10011100=01100011。