基于投入产出技术的省域碳足迹及省际碳转移核算研究成果

空间相关分析方法是描述和显示空间分布、识别异常空间位置和发现隐含空间关系等的一系列技术的集合，其核心是空间自相关性的测度，包括全局和局部空间自相关两大类。

（1）全局的空间相关性，又称全局空间自相关，主要分析区域总体的空间关联和空间差异程度。其中，全局Moran's Ⅰ指标是较为常用的全局空间自相关统计量的估计，其表达式为：

其中，Moran's Ⅰ为全局空间自相关系数；n为研究区域的空间样本个数，即空间位置的个数；xi和xj是空间位置i和j的观察值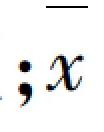为x的平均值；wij为观察省域i和j邻接空间权重矩阵，当i和j为邻近的空间位置时，wij=1，反之，wij=0。

全局Moran's Ⅰ的取值范围为［-1，1］，如果区域间为空间正相关，则其数值大于0；如果区域为负相关，则其数值小于0；当指数为0时，说明区域间不存在空间自相关性，或者表示属性是随机分布的。当目标区域在空间区位和属性上都相似时，就显示出正的空间相关性，反之则显示出负的空间相关性；当属性分布与区位分布相互独立时，指数值为0。(www.xing528.com)

另外，根据Moran's Ⅰ的值可以绘制出空间相关系数的Moran's Ⅰ散点图。该散点图可以通过分成的四个象限的空间依赖模式来识别各个地区及其相邻地区的关系：第一、三象限表示相似值之间的正向空间相关性，第二、四象限表示不同观测值之间的负向空间相关性，当观测值均匀分布在四个象限时表明地区之间是相互独立的，不存在空间自相关性。

（2）局部空间自相关。全局空间自相关分析揭示了某一属性在整体上的空间依赖程度，但并不能对该属性的局部空间差异性进行分析。当存在显著全局空间自相关性的时候，可能会存在完全随机分布的样本子集。当不存在显著全局空间自相关性的时候，则样本数据子集可能是显著局部相关的。此外，当需要进一步分析属性特征值的高值或低值是否存在局部空间集聚的时候，就有必要进行局部空间自相关分析。因此，Anselin（1995）提出利用局部空间自相关的方法来衡量某一区域与周边之间的空间差异程度及显著性，并结合Moran's Ⅰ散点图或局部空间自相关聚集图等形式研究局部空间分布规律。空间位置为i的局部Moran's Ⅰl的计算公式为：

局域空间自相关其本质就是将Moran's Ⅰ分解到各个区域单元，区域i的局部Moran's Ⅰ指数用来度量区域i和它相邻区域之间的关联程度。在指定的显著性水平前提下，Ⅰl大于零表明存在正的局部空间自相关，相似值发生集聚；否则表明存在负的局部空间自相关，不相似的值发生集聚。