设X1,X2,…,Xn是来自总体X的简单随机样本,θ是总体的未知参数.
(1)θ的矩估计量的计算方法
θ的矩估计量通常按以下方法计算:
计算EX,并令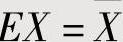 ,由此算出θ,即为θ的矩估计量θ^.
,由此算出θ,即为θ的矩估计量θ^.
(2)最大似然估计量的计算方法
设X1,X2,…,Xn的观察值为x1,x2,…,xn,构造似然函数
L(θ)=f(x1;θ)f(x2;θ)…f(xn;θ)(其中f(xi;θ)是xi的概率密度).
对lnL(θ)求导,且令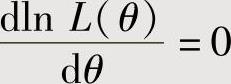 ,解此方程得到的θ=θ(x1,x2,…,xn).将其中的x1,x2,…,xn对应地换成X1,X2,…,Xn,即算得θ的最大似然估计量.
,解此方程得到的θ=θ(x1,x2,…,xn).将其中的x1,x2,…,xn对应地换成X1,X2,…,Xn,即算得θ的最大似然估计量.
例15.1 设X1,X2,…,Xn为来自正态总体N(μ0,σ2)的简单随机样本,其中μ0已知,σ2>0未知.X与S2分别表示样本均值和样本方差.
(1)求参数σ2的最大似然估计量 ;
;
(2)计算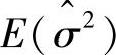 和
和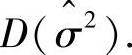
精解 (1)总体的概率密度为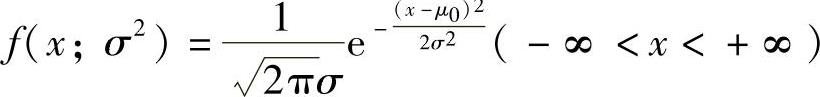 ,记样本的观察值为x1,x2,…,xn,则似然函数为
,记样本的观察值为x1,x2,…,xn,则似然函数为
即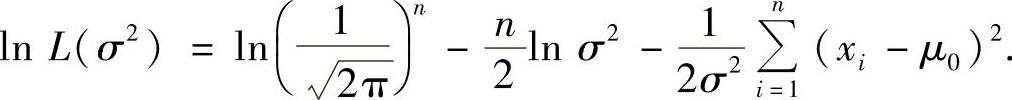
由此得到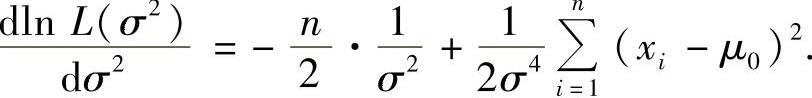
令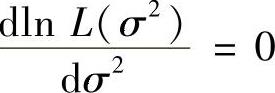 得
得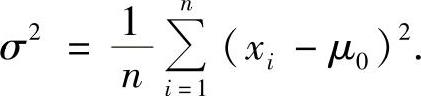 从而σ2的最大似然估计量为
从而σ2的最大似然估计量为
(2)由于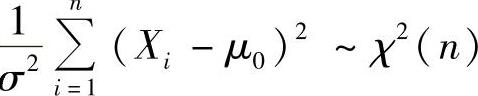 ,所以
,所以
例15.2 设总体X的概率密度为
其中参数λ未知,X1,X2,…,Xn是来自总体X的简单随机样本.
(1)求参数λ的矩估计量;
(2)求参数λ的最大似然估计量.
精解 (1)X的数学期望为
令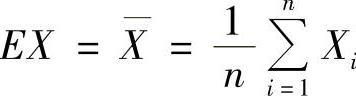 ,即
,即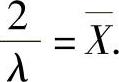 由此得到λ的矩估计量为
由此得到λ的矩估计量为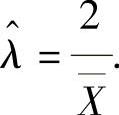
(2)记X1,X2,…,Xn的观察值为x1,x2,…,xn,则似然函数
显然L(λ)只能在x1,x2,…,xn>0时才能取到最大值,所以可以化简L(λ)为
即 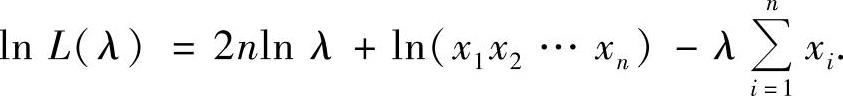
由此可得  (https://www.xing528.com)
(https://www.xing528.com)
令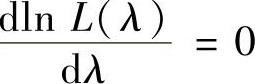 得
得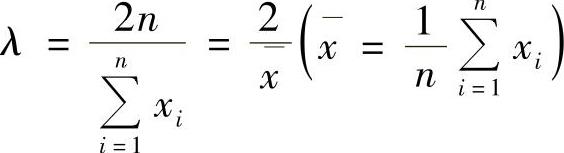 ,因此λ的最大似然估计量为
,因此λ的最大似然估计量为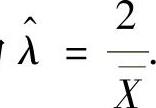
其中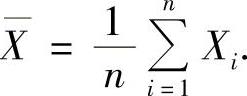
例15.3 (1)设总体X的概率密度为
其中θ(0<θ<1)未知,X1,X2,…,Xn是来自总体X的简单样本,X是样本均值.求θ的矩估计量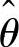 ;
;
(2)设总体X的概率密度为
其中θ>0是未知参数.设X1,X2,…,Xn是来自X的一个简单随机样本,求θ的最大似然估计量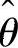 ,并求
,并求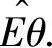
精解 (1)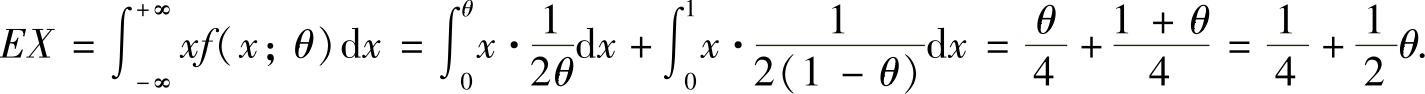
令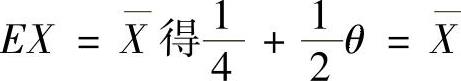 ,所以θ的矩估计量为
,所以θ的矩估计量为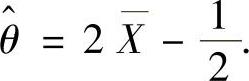
(2)记样本的观察值为x1,x2,…,xn,作似然函数
显然L(θ)的最大值只能在x1,x2,…,xn≥θ处取到,所以可以简化L(θ)为
显然它是θ的单调增加函数,在θ=min{x1,x2,…,xn}处取最大值.从而θ的最大似然估计量为
由于X的分布函数为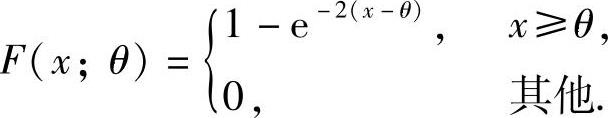 所以X(1)的分布函数
所以X(1)的分布函数
因此,X(1)的概率密度为
从而
例15.4 设总体X的分布函数为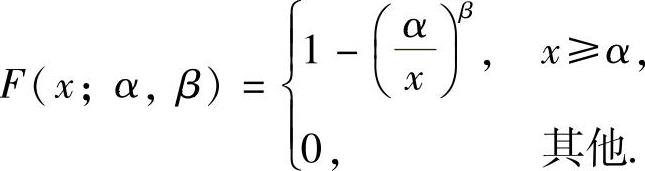 其中参数α>0,β>1.设X1,X2,…,Xn是来自总体X的简单随机样本,
其中参数α>0,β>1.设X1,X2,…,Xn是来自总体X的简单随机样本,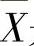 是该样本的均值.
是该样本的均值.
(1)当α=1时,求β2的矩估计量;
(2)当β=2时,求α的最大似然估计量.
精解 X的概率密度为
(1)当α=1时,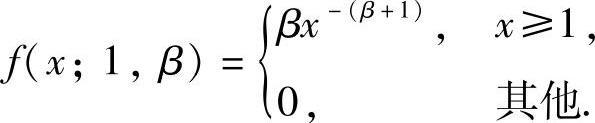 所以
所以
令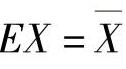 ,即
,即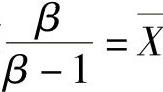 解此方程得
解此方程得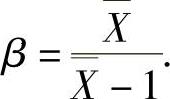 从而β2的矩估计量为
从而β2的矩估计量为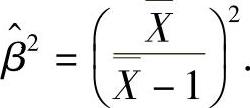
(2)当β=2时,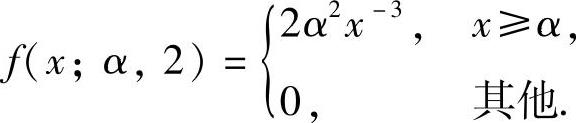 记样本的观察值为x1,x2,…,xn,则似然函数
记样本的观察值为x1,x2,…,xn,则似然函数
显然L(α)的最大值只能在x1,x2,…,xn≥α上取到,所以可化简似然函数为
L(α)=2nα2n(x1x2…xn)-3, x1,x2,…,xn≥α.
容易知道L(α)是单调增加函数,所以当α=min{x1,x2,…,xn}时L(α)取最大值.
因此,α的最大似然估计量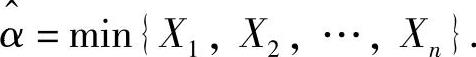
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




