高效的二次型化标准与规范形方法

设n元二次型f（x₁，x₂，…，x_n）=x^TAx（其中x=（x₁，x₂，…，x_n）^T，A是n阶实对称矩阵）.

11.1二次型化标准形

二次型f（x₁，x₂，…，x_n）=x^TAx化标准形有两种方法：

（1）正交变换法

通过正交变换x=Qy（其中y=（y₁，y₂，…，y_n）^T，Q是n阶正交矩阵），将f（x₁，x₂，…，x_n）化为标准形λ₁y²₁+λ₂y²₂+…+λ_ny²_n.

这里的Q和λ₁，λ₂，…，λ_n（它们都是A的特征值）可从A正交相似对角化中算出，即

（2）可逆线性变换法

通过可逆线性变换x=Cy（其中y=（y₁，y₂，…，y_n）^T，C是n阶可逆矩阵），将f（x₁，x₂，…，x_n）化为标准形d₁y²₁+d₂y²₂+…+d_ny²_n.

这里的C和d₁，d₂，…，d_n可从A合同对角化中算出，即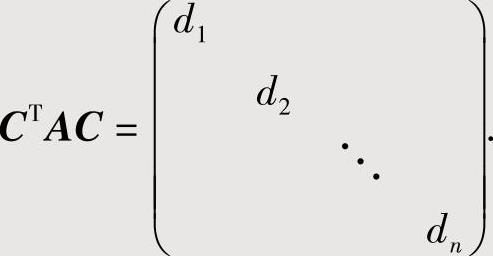具体可对f进行配方得x=Cy.

11.2二次型化规范形

将二次型f（x₁，x₂，…，x_n）=x^TAx化规范形的步骤如下：

（1）将二次型f化为标准形，设为f=c₁y²₁+c₂y²₂+…+c_ny²_n.

（2）当c₁>0时，令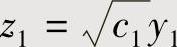；当c₁<0时，令；当c₁=0时，令z₁=y1.对其余变量也同样考虑.如此即得f的规范形

z²₁+z²₂+…+z_p²-z_p+1²-z_p+2²-…-z_p+q²+0·z_p+q+1²+…+0·z²_n.

其中p称为f的正惯性指数，q称为f的负惯性指数，显然p+q=r（A）.

惯性定理 任意二次型f（x₁，x₂，…，x_n）=x^TAx总可以经过适当的可逆线性变换化成规范形，其规范形是唯一的，与所选的可逆线性变换无关，即正平方项个数p，负平方项个数q由f唯一确定.

例11.1 已知二次型f（x₁，x₂，x₃）=x^TAx （x=（x₁，x₂，x₃）^T，A是三阶实对称矩阵），在正交变换x=Qy （y=（y₁，y₂，y₃）^T，Q是正交矩阵）下的标准形为y²₁+y²₂，且Q的第3列为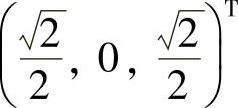，求f（x₁，x₂，x₃）.

精解 实际上只要算出A即可.

由题设知A有特征值为λ=1（二重）和λ=0，且对应λ=0的特征向量为ξ₃=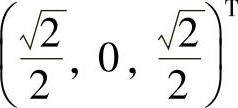，于是由A是实对称矩阵知，对应λ=1的特征向量α=（a，b，c）^T应满足

从而可取α=ξ₁=（0，1，0）^T和α=ξ₂=（-1，0，1）^T.

显然ξ₁，ξ₂，ξ₃两两正交，现将它们单位化：

于是

并且

从而

所以所求的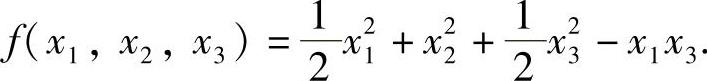

例11.2 设二次型f（x₁，x₂，x₃）=ax²₁+ax²₂+（a-1）x²₃+2x₁x₃-2x₂x₃.

（1）求f的矩阵的所有特征值；

（2）若f的规范形为y²₁+y²₂，求a的值.

精解 （1）由于f的矩阵为

所以由

得A的特征值为a-2，a，a+1（由小到大排列）.

（2）由f的规范形是y²₁+y²₂，所以A有两个正特征值和一个零特征值，从而a-2=0，即a=2.

例11.3 已知二次型f（x₁，x₂，x₃）=（1-a）x²₁+（1-a）x²₂+2x²₃+2（1+a）x₁x₂的秩为2.

（1）求a的值；

（2）求正交变换x=Qy，把f（x₁，x₂，x₃）化为标准形；

（3）求方程f（x₁，x₂，x₃）=0的解.

精解 （1）f的秩即为它的矩阵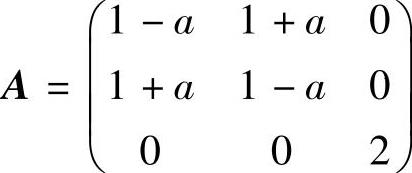的秩，所以由题设知r（A）=2.从而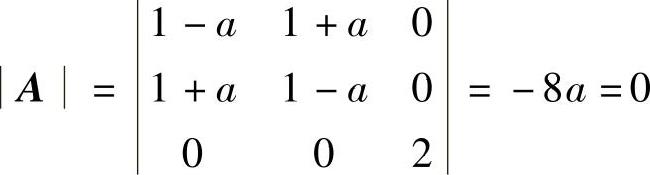，由此得到a=0.(www.xing528.com)

（2）将a=0代入A得

记三阶单位矩阵为E，则由

得A的特征值为λ=0，2（二重）.

记对应λ=0的特征向量为ξ₁=（a₁，a₂，a₃）^T，则它满足

所以可取ξ₁=（1，-1，0）^T.

设对应λ=2的特征向量为ξ₂=（b₁，b₂，b₃）^T，则由A是实对称矩阵知

ξ₁·ξ₂=0，即b₁-b₂=0，

所以可以取ξ₂=α₂=（1，1，0）^T，ξ₃=α₃=（0，0，1）^T.

显然，ξ₁，α₂，α₃两两正交，现将它们单位化：

记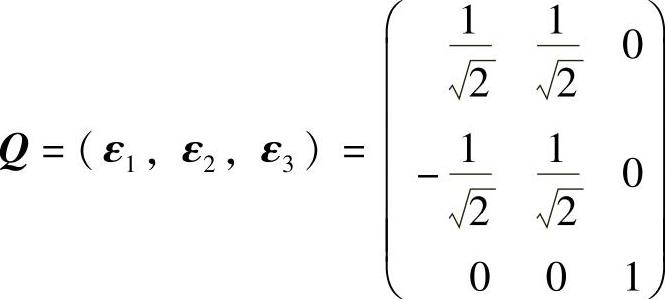（正交矩阵），则x=Qy（其中y=（y₁，y₂，y₃）^T）将f（x₁，x₂，x₃）化为标准形，即f=2y²₂+2y²₃.

（3）由（2）知f（x₁，x₂，x₃）=0即为2y²₂+2y²₃=0.由此得到

y₁=k（任意常数），y₂=y₃=0.

因此由

得f（x₁，x₂，x₃）=0的解为x₁=c，x₂=-c，

例11.4 设二次型f（x₁，x₂，x₃）=x²₁+x²₂+x²₃+2αx₁x₂+2βx₂x₃+2x₁x₃.

（1）经正交变换x=Qy（其中x=（x₁，x₂，x₃）^T，y=（y₁，y₂，y₃）^T，Q是正交矩阵）化成标准形f=y²₂+2y²₃，求常数α，β；

（2）经可逆线性变换x=Py（其中P是可逆矩阵）化为标准形f=y²₂+2y²₃，求常数α，β.

精解 记f=x²₁+x²₂+x²₃+2αx₁x₂+2βx₂x₃+2x₁x₃的矩阵为A，则

（1）经正交变换x=Qy后f=y²₂+2y²₃知A有特征值λ=0，1，2.于是有

其中E是三阶单位矩阵.

由式（1）得（α-β）2=0，即α=β.

由式（2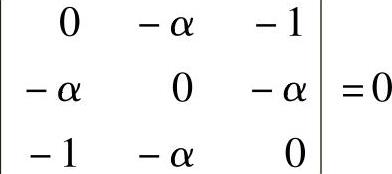）（这里已把β=α代入）得α=0.

因此所求的α，β均为零.

（2）经过可逆线性变换x=Py后f=y²₂+2y²₃知A的秩为2（此时，A未必有特征值λ=0，1，2）.于是对A施行初等变换

知 β-α=0且1-α²≠0，即α=β，但它们都不能为-1及1.

例11.5 设二次型f（x₁，x₂，x₃）=ax²₁+2x²₂-2x²₃+2bx₁x₂（b>0）经正交变换x=Qy（其中x=（x₁，x₂，x₃）^T，y=（y₁，y₂，y₃）^T，Q是3阶正交矩阵）后化为标准形f=λ₁y²₁+λ₂y²₂+λ₃y²₃，其中λ₁+λ₂+λ₃=1，λ₁λ₂λ₃=-4.

（1）求常数a，b的值；

（2）用可逆线变换将f（x₁，x₂，x₃）化为规范形，并求出这个可逆线性变换.

精解 （1）f的矩阵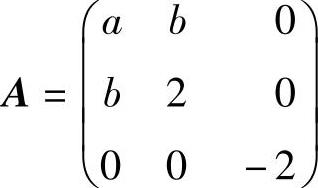，λ₁，λ₂，λ₃是它的特征值，于是由题设知

由此可得a=1，b=2（利用b>0）.

（2）将a=1，b=2代入f（x₁，x₂，x₃），并对它配方得

f（x₁，x₂，x₃）=x²₁+2x²₂-2x²₃+4x₁x₂

=（x²₁+4x₁x₂+4x²₂）-2x²₂-2x²₃

=（x₁+2x₂）2-2x²₂-2x²₃.

于是令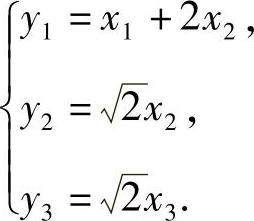则f（x₁，x₂，x₃）=y²₁-y²₂-y²₃（规范形），并且所求的可逆线性变换为