向量组线性相关判定-2016考研数学真题精讲与热点分析

8.1向量组线性相关与线性无关的判定

判定向量组α₁，α₂，…，α_s线性相关与线性无关可以按定义进行，即如果存在一组不全为零的数λ₁，λ₂，…，λ_s，使得

λ₁α₁+λ₂α₂+…+λ_sα_s=0 （∗）

成立，则α₁，α₂，…，α_s线性相关；如果仅当λ₁，λ₂，…，λ_s全为零时，式（∗）才成立，则α₁，α₂，…，α_s线性无关.

判定向量组α₁，α₂，…，α_s线性相关与线性无关还可以从计算秩r（α₁，α₂，…，α_s）入手，即向量组α₁，α₂，…，α_s线性相关（线性无关）的充分必要条件是r（α₁，α₂，…，α_s）<s（r（α₁，α₂，…，α_s）=s）.

8.2向量（或向量组）可否由另一个向量组线性表示的判定

设向量β及向量组α₁，α₂，…，α_s（它们的维数与β相同），则β可由α₁，α₂，…，α_s线性表示的充分必要条件是r（α₁，α₂，…，α_s）=r（α₁，α₂，…，α_s，β）.

设向量组β₁，β₂，…，β_t与向量组α₁，α₂，…，α_s（它们的维数与β₁相同），则β₁，β₂，…，βt可由α₁，α₂，…，α_s线性表示的充分必要条件是r（α₁，α₂，…，α_s）=r（α₁，α₂，…，α_s，β₁，β₂，…，β_t）.

显然，当向量组β₁，β₂，…，β_t可由向量组α₁，α₂，…，α_s线性表示时有

r（β₁，β₂，…，β_t）≤r（α₁，α₂，…，α_s）；

当向量组β₁，β₂，…，β_t与向量组α₁，α₂，…，α_s等价（即可相互线性表示）时有

r（β₁，β₂，…，β_t）=r（α₁，α₂，…，α_s）.

例8.1 计算下列各题：

（1）设向量组α₁，α₂，α₃线性无关，且

β₁=（k-1）α₁+α₂+α₃，β₂=α₁+（k+1）α₂+α₃，β₃=-α₁-（1+k）α₂+（1-k）α₃，求使向量组β₁，β₂，β₃线性无关的k值.

（2）已知向量组（Ⅰ）：α₁=（1，0，2）T，α₂=（1，1，3）T，α₃=（1，-1，a+2）T和向量组（Ⅱ）：β₁=（1，2，a+3）T，β₂=（2，1，a+6）T，β₃=（2，1，a+4）T，求使（Ⅰ）与（Ⅱ）等价的a的值.

精解 （1）由于α₁，α₂，α₃线性无关，所以使β₁，β₂，β₃线性无关的k值应满足r（β₁，β₂，β₃）=3即为

所以k≠2，且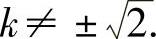

（2）由（Ⅰ）与（Ⅱ）等价知

r（α₁，α₂，α₃）=r（β₁，β₂，β₃）.对（β₁，β₂，β₃）施行初等行变换得

所以 r（Ⅱ）=3.

对（α₁，α₂，α₃）施行初等行变换得

所以，由r（α₁，α₂，α₃）=r（Ⅱ）=3，得a+1≠0，从而a≠-1.

例8.2 （1）设向量组α₁=（1，0，1）T，α₂=（0，1，1）T，α₃=（1，3，5）T不能由向量组β₁=（1，1，1）T，β₂=（1，2，3）T，β₃=（3，4，a）T线性表示，求a的值.

（2）已知向量组α₁=（1，0，2，4）T，α₂=（1，1，3，0）T，α₃=（2，1，a+2，4）T，α₄=（2，-1，3，a+7）T，β₁=（3，-1，a+6，a+11）T，β₂=（0，1，2，a）T.如果β₁可由α₁，α₂，α₃，α4线性表示，但β₂不能由α₁，α₂，α₃，α₄线性表示，求a的值.

精解 （1）由向量组α₁，α₂，α₃不能由β₁，β₂，β₃线性表示知

r（β₁，β₂，β₃）<r（β₁，β₂，β₃，α₁，α₂，α₃）. （1）

对（β₁，β₂，β₃，α₁，α₂，α₃）施行初等行变换：

所以，由式（1）得 a-5=0，即a=5（此时r（β₁，β₂，β₃）=2，r（β₁，β₂，β₃，α₁，α₂，α₃）=3）.

（2）由β₁可由α₁，α₂，α₃，α₄线性表示知

r（α₁，α₂，α₃，α₄）=r（α₁，α₂，α₃，α₄，β₁）， （2）

由β₂不可由α₁，α₂，α₃，α₄线性表示知

r（α₁，α₂，α₃，α₄）<r（α₁，α₂，α₃，α₄，β₂）. （3）

对（α₁，α₂，α₃，α₄，β₁，β₂）施行初等行变换：

所以，由式（2）得a≠3；由式（3）得a=3，5.综合上述两种情形知，β₁可由α₁，α₂，α₃，α₄线性表示，β₂不能由α₁，α₂，α₃，α₄线性表示时，a=5.

例8.3（单项选择题） 设α₁，α₂，…，α_s均为n维列向量，A是m×n矩阵，则下列命题正确的是(www.xing528.com)

（A）若α₁，α₂，…，α_s线性相关，则Aα₁，Aα₂，…，Aα_s线性相关.

（B）若α₁，α₂，…，α_s线性相关，则Aα₁，Aα₂，…，Aα_s线性无关.

（C）若α₁，α₂，…，α_s线性无关，则Aα₁，Aα₂，…，Aα_s线性相关.

（D）若α₁，α₂，…，α_s线性无关，则Aα₁，Aα₂，…，Aα_s线性无关. [ ]

精解 用定义判定正确的选项.

设α₁，α₂，…，α_s线性相关，则存在一组不全为零的常数λ₁，λ₂，…，λ_s，使得λ₁α₁+λ₂α₂+…+λ_sα_s=0，从而

λ₁Aα₁+λ₂Aα₂+…+λ_sAα_s=A（λ₁α₁+λ₂α₂+…+λ_sα_s）=0，所以Aα₁，Aα₂，…，Aα_s线性相关.

因此本题选（A）.

例8.4（单项选择题） 设A，B为满足AB=O的任意两个非零矩阵，则必有

（A）A的列向量组线性相关，B的行向量组线性相关.

（B）A的列向量组线性相关，B的列向量组线性相关.

（C）A的行向量组线性相关，B的行向量组线性相关.

（D）A的行向量组线性相关，B的列向量组线性相关. [ ]

精解 记A=（α₁，α₂，…，α_s）（α₁，α₂，…，α_s是A的列向量组），由于B≠O，所以不妨设

中的第1列是非零列，则由AB=O知，存在不全为零的数b₁₁，b₂₁，…，b_s1，使得

b₁₁α₁+b₂₁α₂+…+b_s1α_s=0.

由此推出A的列向量组线性相关.

由AB=O得B^TA^T=O.同样可证B^T的列向量组线性相关，即B的行向量组线性相关.

因此本题选（A）.

例8.5（单项选择题） 设向量组（Ⅰ）：α₁，α₂，…，α_r可由向量组（Ⅱ）：β₁，β₂，…，β_s线性表示，则

（A）若（Ⅰ）线性无关，则r≤s.

（B）若（Ⅰ）线性相关，则r>s.

（C）若（Ⅱ）线性无关，则r≤s.

（D）若（Ⅱ）线性相关，则r>s. [ ]

精解 设（Ⅰ）线性无关，则r（α₁，α₂，…，α_r）=r.于是由（Ⅰ）可由（Ⅱ）线性表示知r（α₁，α₂，…，α_r）≤r（β₁，β₂，…，β_s）≤s.由此推得r≤s.

因此本题选（A）.

例8.6（单项选择题） 设n维列向量组α₁，α₂，…，α_m（m<n）线性无关，则n维列向量组β₁，β₂，…，β_m也线性无关的充分必要条件是

（A）向量组α₁，α₂，…，α_m可由向量组β₁，β₂，…，β_m线性表示.

（B）向量组β₁，β₂，…，β_m可由向量组α₁，α₂，…，α_m线性表示.

（C）向量组α₁，α₂，…，α_m与向量组β₁，β₂，…，β_m等价.

（D）矩阵A=（α₁，α₂，…，α_m）与矩阵B=（β₁，β₂，…，β_m）等价. [ ]

精解 由于两个n×m矩阵A与B等价的充分必要条件是r（A）=r（B），故从选项（D）入手考虑.

β₁，β₂，…，β_m线性无关的充分必要条件是r（B）=r（β₁，β₂，…，β_m）=m.由于α₁，α₂，…，α_m线性无关，所以上述的充分必要条件是r（A）=r（B），即n×m矩阵A与B等价.

因此本题选（D）.