6.1幂级数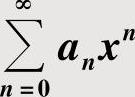 收敛域的计算方法
收敛域的计算方法
收敛域不为{0}的幂级数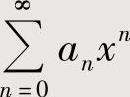 的收敛域可按以下步骤计算:
的收敛域可按以下步骤计算:
(1)用以下方法算出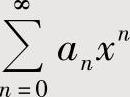 的收敛区间:
的收敛区间:
如果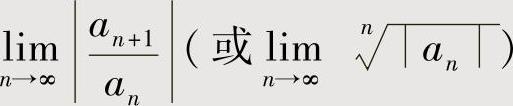 存在为ρ,则当ρ≠0时,
存在为ρ,则当ρ≠0时,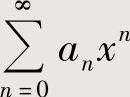 的收敛区间为
的收敛区间为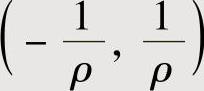 ;当ρ=0时,
;当ρ=0时,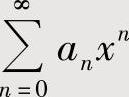 的收敛区间为(-∞,+∞).
的收敛区间为(-∞,+∞).
如果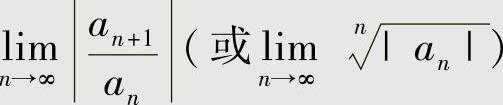 不存在
不存在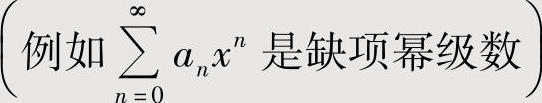 时,将
时,将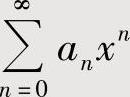 理解成
理解成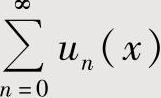 (其中对n=0,1,2,…,un(x)不恒为零),然后计算
(其中对n=0,1,2,…,un(x)不恒为零),然后计算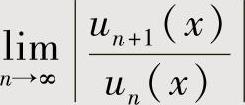 (或
(或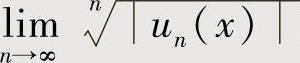 ),如果它们为ρ(x),则收敛区间为{xρ(x)<1}.
),如果它们为ρ(x),则收敛区间为{xρ(x)<1}.
(2)由收敛区间计算收敛域:
当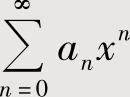 的收敛区间为(-∞,+∞)时,收敛域也为(-∞,+∞).
的收敛区间为(-∞,+∞)时,收敛域也为(-∞,+∞).
当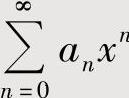 的收敛区间为(-R,R)(R>0)时,考虑
的收敛区间为(-R,R)(R>0)时,考虑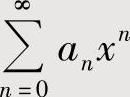 在点x=-R,R处的收敛性,将其中的收敛点并入收敛区间即得收敛域.
在点x=-R,R处的收敛性,将其中的收敛点并入收敛区间即得收敛域.
例6.1 求幂级数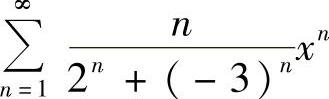 的收敛域.
的收敛域.
精解 记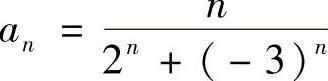 ,则
,则
所以,所给幂级数的收敛区间为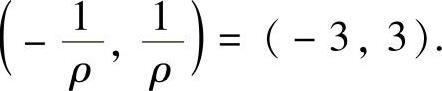
当x=-3,3时,所给幂级数分别为
由于这两个级数的通项都不为零,所以发散.因此所给幂级数的收敛域为(-3,3).6.2幂级数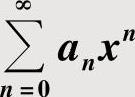 的和函数的计算方法
的和函数的计算方法
幂级数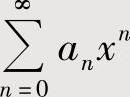 的和函数可以按以下方法计算:
的和函数可以按以下方法计算:
(1)对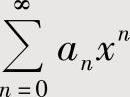 进行适当的代数运算
进行适当的代数运算
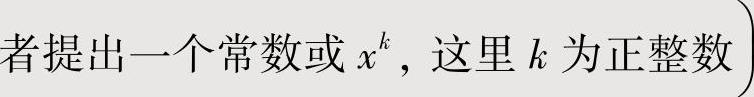 ,或作适当的变量代换,使其成为常用函数(指eax,sinax,cosax,ln(1+ax),(1+ax)μ,这里a,μ都是常数)的麦克劳林级数,从而求得
,或作适当的变量代换,使其成为常用函数(指eax,sinax,cosax,ln(1+ax),(1+ax)μ,这里a,μ都是常数)的麦克劳林级数,从而求得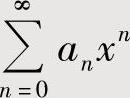 的和函数.有时将
的和函数.有时将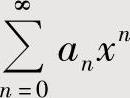 表示成几个幂级数之和,然后对每个幂级数都作以上处理,由此算得
表示成几个幂级数之和,然后对每个幂级数都作以上处理,由此算得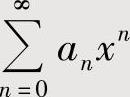 的和函数.(https://www.xing528.com)
的和函数.(https://www.xing528.com)
(2)对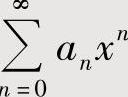 在收敛区间内进行求导数或求二阶导数,或求积分,即
在收敛区间内进行求导数或求二阶导数,或求积分,即
使其成为某个常用函数的麦克劳林级数,由此通过积分、二次积分或求导算得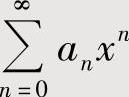 的和函数.
的和函数.
例6.2 求幂级数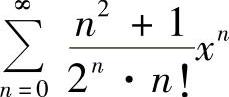 的收敛域与和函数.
的收敛域与和函数.
精解 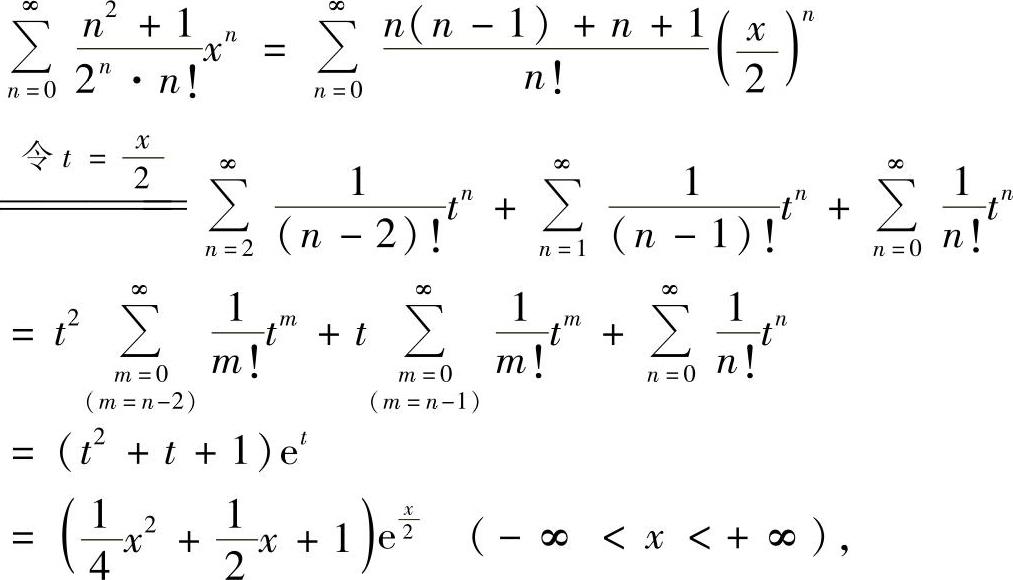 所以,所给幂级数的收敛域为(-∞,+∞),和函数
所以,所给幂级数的收敛域为(-∞,+∞),和函数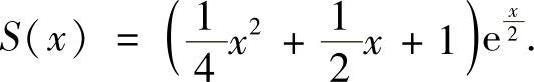
例6.3 求下列幂级数的收敛域与和函数:
精解 (1)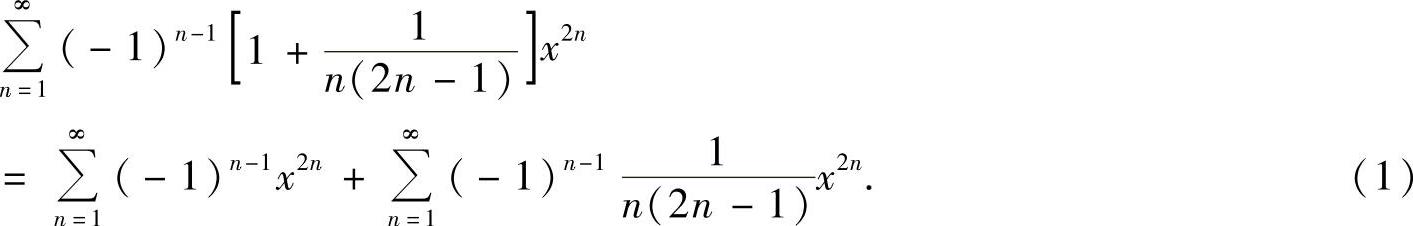
显然,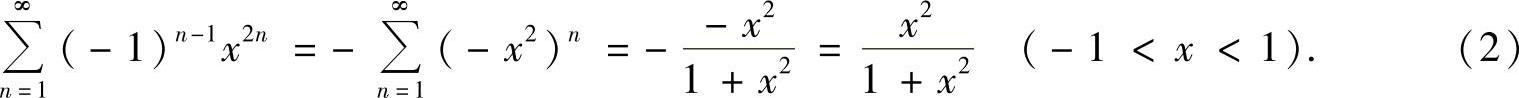
此外,对x∈(-1,1),记
则
所以
将式(2)、式(3)代入式(1)得
(2)记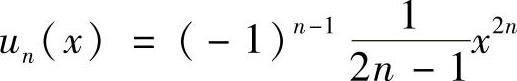 ,则
,则
所以,所给幂级数的收敛区间为(-1,1).由于x=-1,1时,所给幂级数都为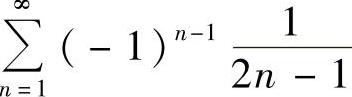 ,收敛.因此收敛域为[-1,1].对x∈[-1,1],有
,收敛.因此收敛域为[-1,1].对x∈[-1,1],有
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




