【摘要】：定积分计算的基础是定积分基本性质、基本积分公式及牛顿-莱布尼茨公式，但还应掌握一些计算方法，以便快捷地算出定积分.4.1换元积分法如果，则作变量代换，当它容易计算时，就算得如果不能作上述处理时，则作适当的变量代换x=φ（t），使得，因此当右边定积分较易计算时，就可算出此外，有时对作适当的变量代换，得到关于I的一个方程，解此方程得到的值；或者将表示成，对其中一个，例如作变量代换而产生一个新的定积分与
定积分计算的基础是定积分基本性质、基本积分公式及牛顿-莱布尼茨公式，但还应掌握一些计算方法，以便快捷地算出定积分.
4.1换元积分法
如果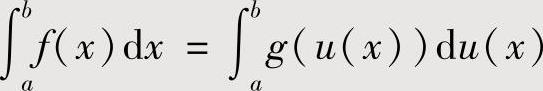
，则作变量代换
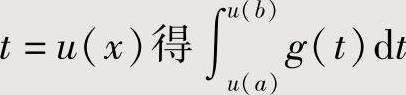，当它容易计算时，就算得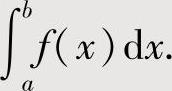
如果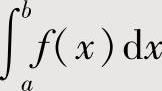
不能作上述处理时，则作适当的变量代换x=φ（t），使得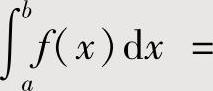
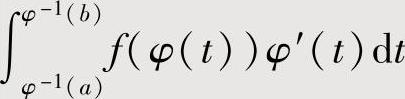，因此当右边定积分较易计算时，就可算出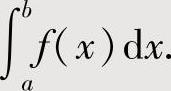
此外，有时对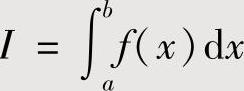
作适当的变量代换，得到关于I的一个方程，解此方程得到
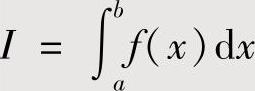的值；或者将
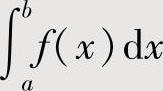表示成
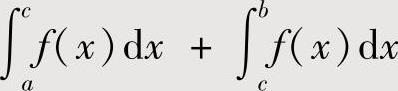，对其中一个，例如
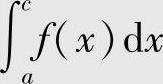作变量代换而产生一个新的定积分与
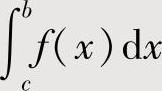抵消，从而算出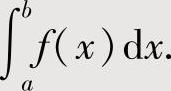
4.2分部积分法
将f（x）dx适当地写成u（x）dv（x），则
如果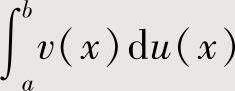
较易计算，则可算出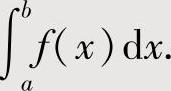
有时，对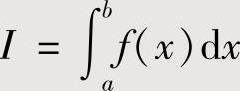
连续使用若干次分部积分法后得到关于I的一个方程，解此方程得到
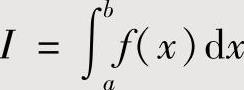的值；或者将I表示成
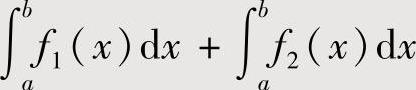，对其中之一，例如
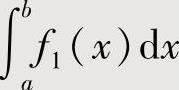施行分部积分法产生的一个新的定积分与
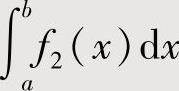抵消，由此算得
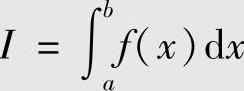的值.
此外，分部积分法往往与换元积分法相结合，有效地计算定积分.
4.3利用奇、偶函数和周期函数的定积分性质计算
设f（x）是[-a，a]上的连续函数，则
设f（x）是连续函数，且以T（T>0）为周期的周期函数，则
例4.1 求下列定积分：
（1）
；
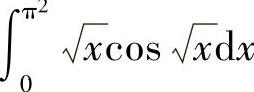（2）
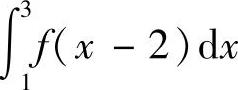，其中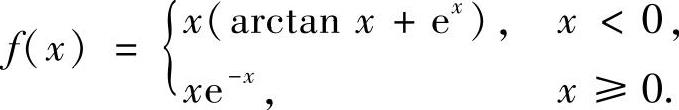
精解 （1）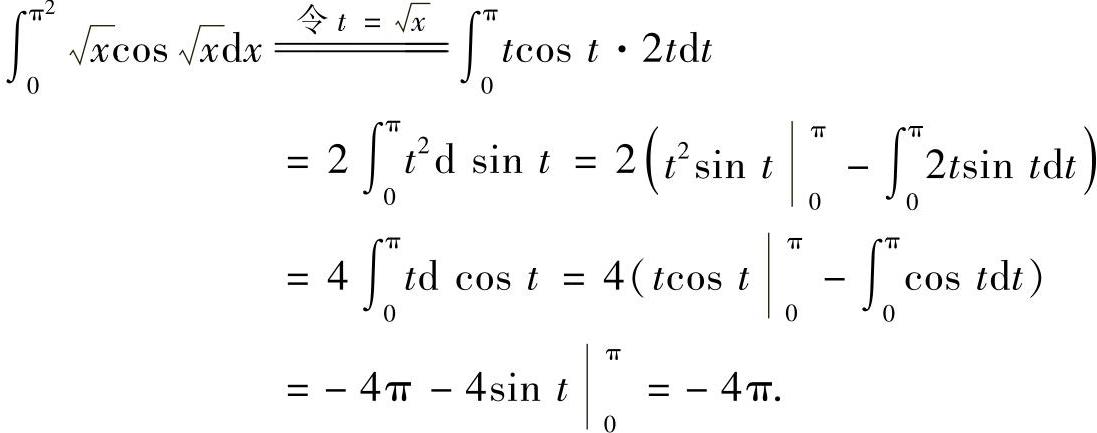
（2）
例4.2 求下列定积分：
（1）
；
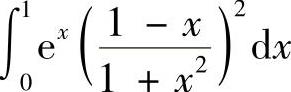（2）
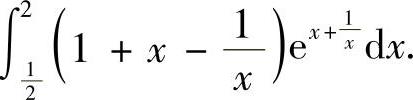(https://www.xing528.com)
精解 （1）
（2）
例4.3 求下列定积分：
（1）
；
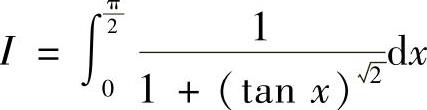（2）
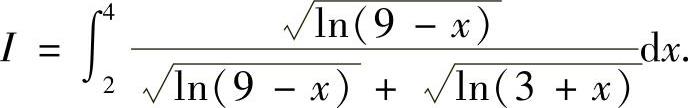
精解 （1）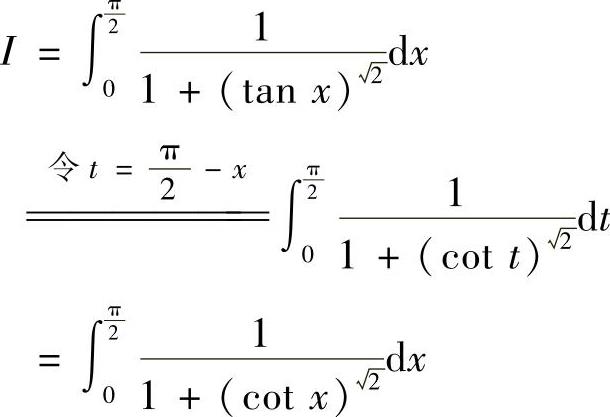
即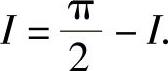
所以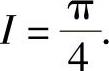
（2）
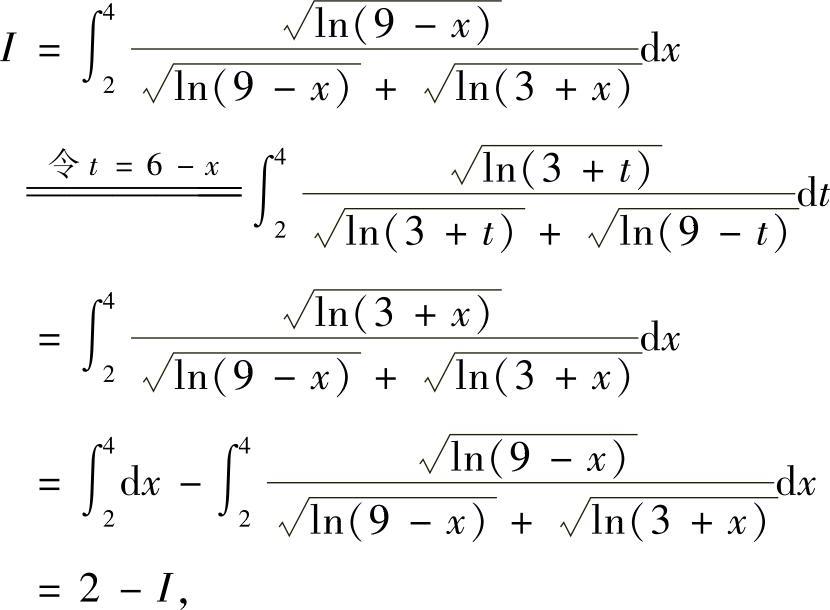
即 I=2-I.所以I=1.
例4.4 计算定积分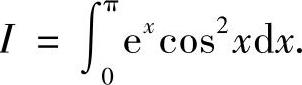
精解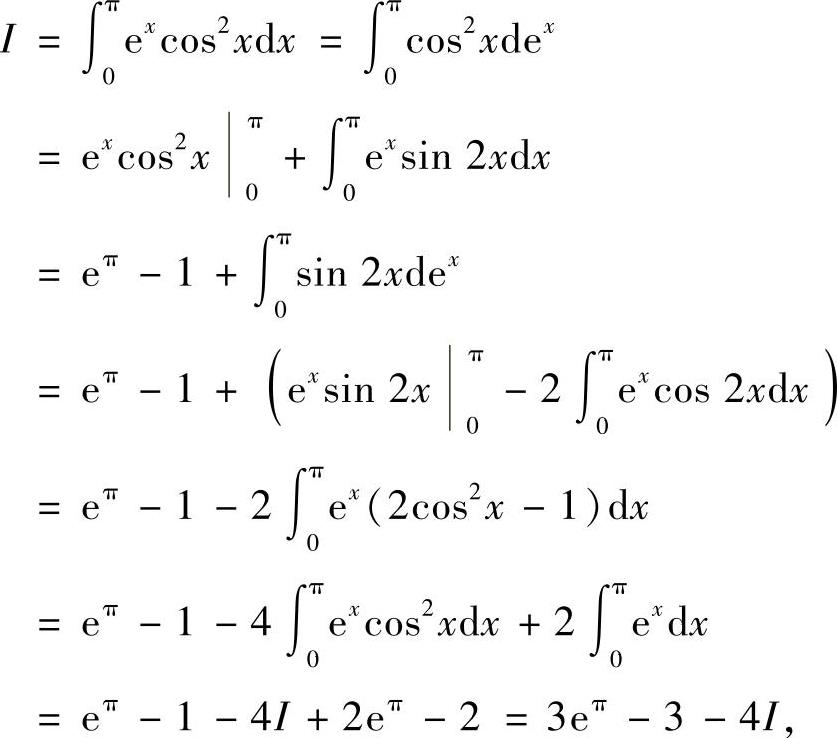 
即I=3eπ-3-4I.所以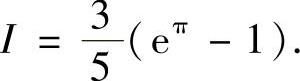
例4.5 计算下列定积分：
（1）
；
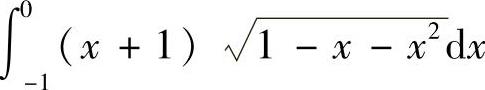（2）
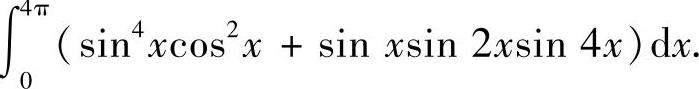
精解 （1）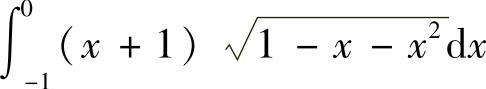
（2）
例4.6 计算定积分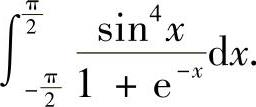
精解 积分区间是对称的，但被积函数是非奇非偶函数，因此将它表示为
所以
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
