跨区域水污染防治合作机制研究成果

政府采取对企业的生产工艺研发和污染减排研发分别进行补贴的技术激励政策时，其博弈过程可以描述为：第一阶段政府预先设定给予企业的研发补贴率，第二阶段企业确定分别用于生产工艺研发和污染减排研发的投入水平，第三阶段企业在产品市场上进行竞争。博弈的均衡解可以通过逆向归纳法求得。补贴政策下企业的成本函数变成如下形式：

其中，d 为生产工艺研发补贴率，s 为污染减排研发补贴率，且0 ＜d，s ＜1，xssi +kxssj ＜c。

在第三阶段，企业在产品市场上展开竞争，选择产量最大化利润，即

由式（9.5）的一阶条件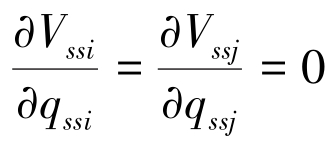，可以得到最优的产量和利润，即

其中，i≠j， i=1，2；A=a-c。将式（9.6）代入式（9.5），可得

由式（9.7）可以看出，最优产量和生产工艺研发水平有关，和污染减排研发水平无关。随着排放税的增加，产量会下降，利润会增加。

在第二阶段，企业选择研发水平最大化利润。对式（9.7）求关于生产工艺研发水平的一阶偏导，由 可解得

在对称均衡条件下有，代入式（9.8）可解得最优生产工艺研发水平，即

其中，9（1 - d） - 2（2 - k）（1 + k） ＞0，A ＞t。

将式（9.9）代入式（9.6），可得

容易证明，这说明排放税越高，生产工艺研发水平和产量就会越低。

对式（9.7）求关于污染减排研发水平的一阶偏导，令可得

由式（9.11）看出，当t=0，yssi =0，表示在不征收排放税的情况下，企业不会采取任何治理污染的措施；随着排放税的提高，企业会更主动、更积极地参与污染治理。

由于企业获得的利润来自生产和污染治理两部分，在对称均衡条件下利润可以表示为(www.xing528.com)

其中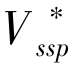， 表示通过生产获得的利润， 表示通过治污获得的利润。

易得

经过整理，企业获得的利润可以表示为

其中，9（1 - d） - 2（2 - k）2 ＞0。

在第一阶段，政府选择补贴率最大化社会福利。福利函数包括生产者剩余和消费者剩余以及产生的环境破坏。为了便于讨论，假定边际破坏成本α = β =，则福利函数为

式（9.14）等价于

将式（9.9）、式（9.10）、式（9.11）代入式（9.15），可得

将式（9.16）最大化，通过一阶条件，可解得生产工艺研发的最优补贴率为

易证，所以生产工艺研发补贴率会随生产工艺研发溢出率的增加而增加。

对式（9.16）求一阶条件，可解得污染减排研发的最优补贴率为

由式（9.18）可以得出，t=0 时，s* = 1，表示在没有征收排放税的情况下，企业不愿意承担污染减排研发的成本，政府承担所有的研发成本。由于表示补贴率会随征收税率的提高而减少，故令s* = 0 可得临界税率t* = A（1 + σ）。当t ≥t*时，s*≤0，政府不提供补贴；t ＜t*时，s* ＞0，同时，表示临界税率随污染减排研发溢出率的提高而提高。

综上，补贴政策下企业的均衡研发水平、利润和社会福利分别为