内部风险的模糊动态夏普利值研究成果

各地区作为局中人进行合作时常常面临诸多不确定的风险因素，主要包括外部风险和内部风险两类。其中外部风险主要来自政治风险、经济风险、自然环境风险等，内部风险主要来自组织风险、资金风险、信息风险、道德风险等。由于每个地区都会面临外部风险，并将平均承担风险带来的影响，因此本章只考虑内部风险的影响。各地区对内部风险的评估值不同，将直接影响参与环境项目投资的积极性。风险越低，参与积极性越高；风险越高，参与积极性越低。为了更加准确地评估风险对各地区参与流域水污染治理的影响，可以通过对每个风险因素发生的概率进行分析，同时赋予每个风险因素权重，利用模糊加权评判法求出风险评估值。首先用评判内部风险的因素构成评判因素集{a1，a2，a3，a4}，其中a1，a2，a3，a4 分别表示组织风险、资金风险、信息风险、道德风险。组织风险表示组织机构建立并启动以后，在运行过程中因为组织的决策、组织、协调和实施等行为失当及偏误所造成的经营风险。资金风险表示地区在生产运营中如果存在占用大量资金，会使资金不能正常运转，造成项目投资中断。信息风险表示在共享信息的过程中，信息的不对称和严重的信息污染现象导致的信息不准确性、滞后性等不良后果。道德风险表示各地区为了自身利益，违背承诺，不遵守协议，在合作中虚报信息，逃避责任，严重威胁和影响正常运作。地区i 的内部风险评判因素集可以表示为{ai1，ai2，ai3，ai4}，其中aij 表示第i 个地区对风险因素j的评判值。根据地区自身的判断标准，对内部风险因素给出相应的权重q1，q2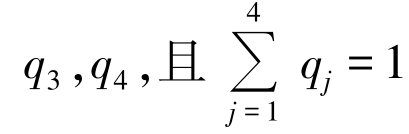，，运用模糊加权评判法即可计算出地区i 对内部风险的评判值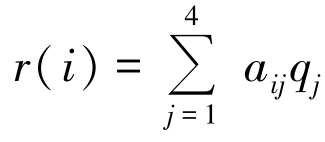。根据风险评判值可以得出可靠值，即各地区的参与度s（i）=1-表示参与水平0 ＜s（i）≤ml的所有局中人组成的清晰联盟[136]。

令Q（s）= {s（i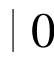） ＜s（i）≤1， i∈s}，q（s）为Q（s）中所含元素的个数，将Q（s）中的元素按照单调非减的顺序排列为m1≤m2≤…≤mq（s）。此时效用函数V（t）s（t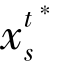，） 是一个模糊测度，可以通过Choquet 积分表示[136]为

其中，l=1，2，…，q（s）； m0=0，mq（s）+1 =0。(www.xing528.com)

在动态夏普利值的基础上考虑风险因素的影响，夏普利值可以改进为

协调转型补贴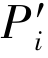（t） 可以表示为