【摘要】：将夏普利值由静态合作扩展到动态合作。在整个合作期间[t0，T]，每个局中人都同意按照夏普利值分配联盟的合作收益。为了让夏普利值在整个合作过程中都得到维持，需要建立一个得偿分配程序，它由协调转型补贴 Pi（τ） 和最优终点支付qi组成[1]。其中 表示在时间为τ、状态为时，局中人约定的合作控制。
将夏普利值由静态合作扩展到动态合作。在整个合作期间[t0，T]，每个局中人都同意按照夏普利值分配联盟的合作收益。因此，在时间为τ，状态为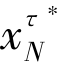
时，局中人i 分得的收益可以表示为[36]
其中，V（τ）s（τ，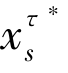
） -V（τ）s\i（τ，
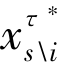） 为局中人i 对联盟s 的价值函数的边际贡献。为了让夏普利值在整个合作过程中都得到维持，需要建立一个得偿分配程序（Payoff Distribution Procedure），它由协调转型补贴（Equilibrating Transitory Compensation） Pi（τ） 和最优终点支付qi（x（T））组成[1]。协调转型补贴Pi（τ） 表示局中人i 在时间点τ 从合作博弈得到的瞬时收益。为了达到帕累托最优，Pi（τ） 需要满足如下条件[36]，即
式（5.2）表示在每一个时间点τ，所有局中人得到的收益总和都必须等于所有局中人在总联盟N 中采用最优合作策略时得到的瞬时收益的总和。其中
表示在时间为τ、状态为
时，局中人约定的合作控制。利用合作收益
的可微分特性，经过数学运算可得[36](www.xing528.com)
式（5. 3）表示当所有局中人都采用根据当前时间和状态而定的最优策略时，每位局中人可以获得的瞬时收益将随着时间和状态的进展而转变，其中
表示时间的最优变化进展； 
表示状态的最优变化进展。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
