二项式半值与联盟结构的影响

局中人在权衡利弊后常常会在大联盟中作出自发形成小联盟的决定，使得大联盟被分割成若干个子联盟，这会对分摊结果带来影响。假设B（N）表示局中人N 中各种分割的集合，每一种分割B ∈B（N）。假设B={B1，B2，…，Bm}为局中人集合的某一联盟结构； M ={1，2，…，m}表示B 的指标集，它满足子集非空性和不相交性，即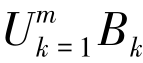 =N，且Bk ∩Bl =∅，k，l ∈{1，2，…，m}，k ≠l。当每个局中人独自构成一个联盟时，则形成了最小的联盟结构，即Bn ={{1}，{2}，…，{n}}；当大联盟形成时，则Bn={{N}}。在联盟结构中，自然形成的二级博弈可表示为（N，C，B），第一阶段博弈是子联盟之间的博弈；第二阶段博弈是各子联盟内部局中人之间的博弈。假设每个局中人分摊的成本为σi（N，C，B），则联盟结构中求解成本的二项式半值可以表示为[133]

若令

则形成矩阵

由此可得

在联盟结构中，利用多重线性扩展法来求解A（i）。首先用函数f （x1，x2，…，xn）表示成本分摊博弈。对于t ∈M，t ≠j，m ∈Bt， 用yt 代替xm，其中，如果出现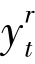（r ＞1），则用yt 代替，由此得到一个关于xk 和yt 的新函数gj（xk，yt），且有(www.xing528.com)

求解gj（xk，yt）关于xi 的偏导数，可得

用αp 代替xk，用αq 代替yt，则有

可以看出

因此