研究：实现跨行政区水污染防治的合作机制

对于任何一个合作博弈，如果博弈中的一位局中人在某时间点的行动依赖于在他之前的行动，那么该博弈便是一个动态合作博弈；反之则为一个静态合作博弈。对于动态合作博弈，如果有两个或两个以上的阶段，那么就是离散动态合作博弈；如果每个阶段的时间差收窄至最小极限，那么博弈便是一个时间不间断的动态合作博弈，又称微分合作博弈[118]。

（1）动态合作博弈

在动态合作博弈中，逆向归纳法（Backward Induction）是其求解的有效方法，即从动态合作博弈的最后一个阶段博弈方的行为开始分析，逐步倒推回前一个阶段相应博弈方的行为选择，一直到第一个阶段的分析方法。动态合作博弈的分析往往为扩展式表述，即采用博弈树的形式，分析要素包括①局中人集合N={1，2，…，n}；②局中人的行动顺序：在什么时候行动；③局中人的行动空间：行动时局中人的选择；④局中人的信息集：行动时局中人知道什么；⑤局中人的得益函数：行动结束后局中人的得益；⑥外生事件：自然选择的概率分析[91]。逆向归纳法的实质就是将多阶段动态合作博弈化为一系列的单阶段合作博弈，通过对一系列的单阶段博弈的分析，确定各博弈方在各自单阶段的选择，最终对动态合作博弈的结果，包括对博弈的路径和各博弈方的得益等作出判断，归纳各博弈方在各阶段的选择，由此可得到各博弈方在整个动态合作博弈中的策略[119]。

（2）微分合作博弈

在微分合作博弈中，每位局中人都愿意遵循各方都同意的最优共识原则（Solution Optimality Principle）来决定如何合作以及如何分配合作得益。最优共识原则解法具体包括两个部分：第一，合作策略（或控制）集合的协议；第二，整体得益的分配方案。在合作博弈中，最优共识原则解法将沿着博弈的合作状态轨迹路径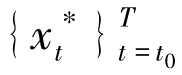 生效，同时还必须符合集体理性和个体理性。集体理性要求参与各方共同议定的合作策略能达到帕累托最优；个体理性要求局中人不会在合作安排下得到较不合作时低的支付[8]。考虑一个n 人合作博弈Γ（x0，T - t0），其中x0 表示博弈的开始状态；t0 和T 分别表示博弈的开始时间和结束时间，T-t0表示博弈的持续时间。每位局中人参与合作必须最大化各自得益的总和，其目标函数的现值可以表示为

其中，t ∈[t0，T] 表示博弈的每一时间点或时刻；ui ∈Ui 表示局中人i 的控制，代表一条随时间进展的策略路径；x（t） ∈X ⊂Rm 表示状态变量，其进展变化取决于动态系统[见式（2.10）]； gi[t，x（t），u1（t），u2（t），…，un（t）] 表示局中人i的瞬时得益；qi（x（T）） 表示局中人i 的终点得益。

根据最大值原理可得最优控制集u（t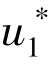）=[（t），…，（t）]，将其代入式（2.10）可得最优状态轨迹，即*

当存在连续可微分函数V t0（t，x）：[t0，T] × Rm →R 时， 满足如下贝尔曼方程（Bellman Equation）[120]

其边际条件为(www.xing528.com)

式中Vt0（t，x） 表示所有局中人在t0 开始的博弈中，在时间和状态分别为t 和x时，其在以后的时区[t，T]的得益总和的现值，亦即整体的价值函数。式（2.12）表示整体的价值函数的值将随着时间的进展而转变，而在每一瞬间的转变的减数则等于整体的瞬时得益的现值，加上状态的最优变化进展为整体价值函数的值所带来的转变。式（2.13）表示整体的价值函数在结束时间点的得益等于整体进行了相应贴现的终点得益。

（3）随机微分合作博弈

考虑一个n 人合作博弈Γ（x0，T - t0），局中人合作的期望目标函数的现值可以表示为

它受制于随机动态系统

在式（2. 14）—式（2. 15）中， Et0 表示局中人在时间点t0 的期望算子；σ[t，x（t）] 表示m × Θ 矩阵；z（t）表示Θ 维的维纳过程；令Ω[t，x（t）] =σ[t，x（t）]σ[t，x（t）]T 表示一个协方差，其中带有行h 和列ξ 的元素记为Ωhξ[t，x（t）]。通过以上元素就可将随机因素加入到微分合作博弈中，则最优状态轨迹 可以表示为

当存在连续可微分函数Vt0（t，x）：[t0，T] × Rm →R，满足以下偏微分方程

其边际条件为

式（2.17）表示整体的价值函数的值将随着时间的进展而随机地转变，而在每一瞬间的转变的减数则相等于整体的瞬时得益的现值，加上状态的最优变化进展为价值函数的值所带来的转变，再加上状态的随机变化进展为价值函数的值所带来的转变。式（2.18）表示整体的价值函数在结束时间点的得益相等于整体进行了相应贴现的终点得益。