径向基网络在非线性协整时间序列中的应用

Broomhead、Lowe（1988）以及Moody与Darken（1988）是最早将径向基函数（RBF）用于神经网络设计的，其采用的是三层前向网络。网络的第二层为隐层，变换函数为RBF，它为一种局部分布的对中心点径向对称衰减的非负非线性函数，一般为高斯函数，形如：

这里，模一般使用欧几里德距离。

图7-4　基于RBF神经网络的非线性函数估计模型

与BP模型所述一样，考虑相同的网络结构如图7-4所示，那么，RBF网络的基本思想为：用RBF作为隐单元的“基”构成隐层空间，设有q个这样的神经元，将输入数据xi＝(xi1,xi2,…,xip)直接（即不通过权连接）映射到隐空间。当RBF的中心cj确定以后，这种映射关系就确定了。而从隐含层空间到输出层空间的映射是线性的，即网络的输出是各隐单元输出的线性加权和，此处的权为网络可调参数。由此，可得输出函数模型为：

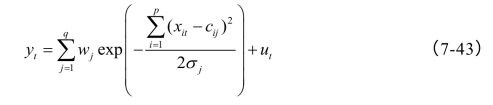
从总体上看，网络从输入到输出的映射是非线性的，而网络的输出则是线性的。这样网络的权就可由线性方程组直接解出或用随机线性搜索法（Random Linear Search，RLS）递推计算，从而大大加快了学习速度并避免了局部极小问题。高斯函数作为隐层节点的激发函数，其学习算法简单实用，收敛速度快。

王春玲（2007）系统比较了RBF神经网络的各种算法：梯度法、K-均值聚类法、正交最小二乘法、动态均值聚类法以及次胜者受罚的竞争学习与基于李雅普诺夫理论的自适应滤波（Rival Penalized Competitive Learning&Lyapunov-theory-based Adaptive Filtering Adaptive Filtering，RPCL-LAF）算法。仿真发现，RPCL-LAF学习算法的性能优越，学习次数少，学习精度高。因此，本书介绍该算法的基本思想和步骤：

RPCL算法由Lei Xu（1993）提出，其基本思想是：对于每个输入值，不仅竞争获胜的单元被修正以适应输入值，而且每次对次胜单元则采用惩罚的方法，使之远离输入值。Kah Phooi Seng等（2002）提出的LAF算法则是通过定义滤波误差和预测误差获得算法的递推公式，算法的稳定性和收敛性可由Lyapunov稳定性理论来保证。对于权值的确定，RLS算法依赖输入信号自相关矩阵的逆，这不仅可以导致大的计算量，而且还可以出现不稳定问题，从而使网络的性能下降，而LAF算法则避免了这些问题。

RPCL-LAF学习算法步骤：

（1）初始化网络。令网络的初始中心数为0，给定参数值：距离门限值ρ，正学习率ηc和反学习率ηr(0﹤ηr≤ηc≤1)。

（2）对于第一个输入样本x1＝(x11,x21,…,x p1)，将其直接作为网络中心，并调用LAF方法进行权值修正。

（3）对于第i个（i＝2,3,…,N ）个输入样本xi＝(x1i,x2i,…,xpi)，求出其与全部中心节点的距离：

（3）找出全部距离中最小者和次小者，即：

这里，第k个和第l个中心分别为获胜单元和次胜单元。(www.xing528.com)

（4）比较dk与距离门限值ρ，若dk﹥ρ，则增加一个中心，其值为该第i个输入样本xi；否则，按下式进行中心修正：

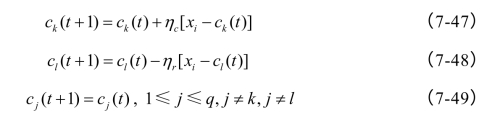
（5）更新中心后，调用LAF方法进行权值修正。

（6）若i≤N，则转至（3），否则，学习结束。

LAF算法步骤如下

对于样本输入xi，隐层单元的输出向量为为隐层单元数，则权值修正为：

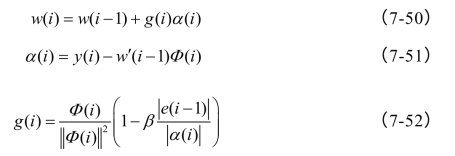
这里0≤β﹤1。

为防止特异性，Kah Phooi Seng建议将式（7-52）改为：

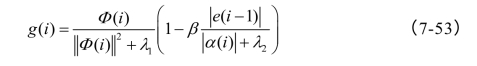
这里λ1与λ2为很小的正数^[4]。

例7-2　考察函数f(x)＝1.1(1－x＋2x2)e－1/2x2，x～U[－4,4]，取样本数为100，应用RPCL-LAF学习算法，神经元个数为11个，迭代300次，逼近效果如图7-5所示：

图7-5　左边为拟合图，曲线为逼近值，点为函数值；右图为适应度变化图^[5]

由图7-5可知，迭代50次的逼近精度已经非常高，迭代300次时的总平均误差则为：3.3126920e-006，这表明应用RPCL-LAF学习算法的径向基神经网络对高斯类函数的逼近效果非常好。

本书MC仿真研究发现，径向基神经网络对于高斯类非线性函数表现出较强的逼近能力，但对于简单的严格单调函数或其他类波动函数，其逼近能力则有待商榷，当输入数据分布较为均匀时，由RPCL算法确定的中心数倾向于过多，而距离门限值ρ的确定难度也降低了该方法的泛化能力。