对于神经网络的学习算法，Rumelhart等（1985）提出了误差反向传播（Error Back Propagation，EBP）算法（简称BP），它系统解决了多层神经网络中隐单元层连接权的学习问题，成为神经网络的重要模型之一，得以广泛使用。Dufrénot与Mignon（2002）研究认为，神经网络估计方法是将可以用来描述给定时间序列的若干个似乎合理的非线性过程组合成一个广义模型，以近似逼近未知的非线性函数。一个神经网络由两类方程组成：第一类方程通常称为隐层或隐单元活动，第二类方程称为输出层。
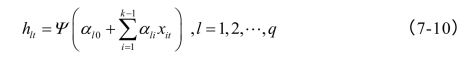
第一类方程给出解释变量的未知非线性函数的形式。假设有q个非线性函数，分别为：其中，假设向量Xt的元素中有一个为内生变量（或称之为被解释变量），其余的(k－1)个为解释变量。事实上，式（7-10）定义了一组不同的非线性函数，从而Ψ(∙)为一向量函数。
第二类方程给出这些不同的非线性函数hl的组合，为：
其中，序列{ut}的最大李雅普诺夫指数为负值；函数Φ(∙)称为活动函数；yt为输出层。
为保证神经网络模型的合理性，而对数据和函数Ψ(∙)与Φ(∙)都给出一些规则和平滑条件，特别地，Ψ(∙)必须为有界函数。在实证分析中，可取Φ(∙)为恒等函数，而Ψ(∙)则为逻辑斯蒂函数：Ψ(x)＝1/(1＋exp(－x))。由此，可得输出函数模型为：
该模型中需要估计的未知参数有q，βl以及αli共2＋(1＋k)q，此外，还需估计每个系数的标准误差和ut的方差。为避免需估计的参数过多，一般取q＝2或者q＝3。对于给定的q，模型（7-12）可用最速梯度下降法、牛顿法和共轭梯度法等算法进行估计。
上述方法为典型的BP神经网络形式，其三层拓扑结构如图7-1所示。
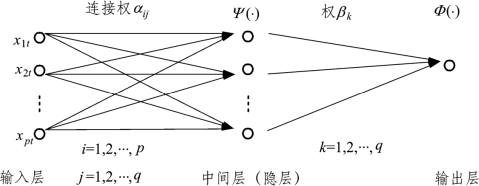
图7-1 基于BP神经网络的非线性函数估计模型
对于中间层（隐层），其基本函数形式有两种：跃阶函数形式和S型（Sigmoid）响应函数，前述常用的逻辑斯蒂函数为Sigmoid响应函数的一种。
对于中间层的数目q，一般来说，隐层的神经元选取数目的原则为：
然而具体到某一复杂问题时，则需考虑自适应方法进行确定，本书将介绍一种剪枝算法。
BP网络具有以任意精度逼近任何非线性连续函数的能力，而且不需要事先确定函数的形式。但是BP网络在实用中存在以下几个主要问题：（1）收敛速度慢，对于一个简单问题也需要成百上千次的学习才能收敛。（2）目标函数存在局部极小点，因此不能保证收敛到全局最小点。（3）网络隐含层的层数及隐含层的单元数选取尚无理论指导，而要根据经验确定。（4）网络的学习和记忆具有不稳定性。
为避免上述问题，Vogl提出“批处理”的思想：按使得全部样本输入值的累积总误差最小的最值梯度下降法修正各节点权值，同时在对权值进行调整时加入动量，并使学习率可自适应调整，即当误差梯度修正方向正确时，就增大学习率从而加强动量项，否则减小学习率从而减弱动量项。
Vogl算法修正了BP算法中的不足，但可能会因学习速率过大导致学习过程振荡，需要实际选择合适的学习率的大小。该算法过程如下：
（1）连接权初始化。将输入层到中间层的连接权矩阵V＝(αij)p×q、各中间层阈值αj0以及中间层到输出层的连接权矩阵W＝(βk)q×1和阈值β0各元素赋予[－1,1]间的随机数。
（2）对于输入值Xt＝(x1t,x2t,…,xpt)′，开始向输出层按式（7-12）逐层计算各神经元的输出：
（3）按最值梯度下降法计算训练误差，从输出层向输入层逐层推算：总误差为：
则按“批处理”思想使总误差最小的梯度法进行各层阈值和权重的调整：
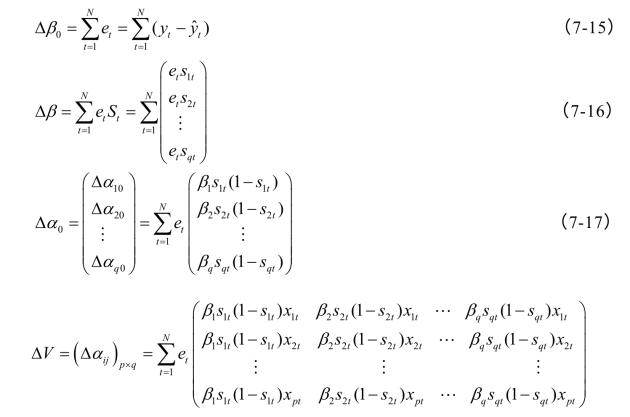
这里
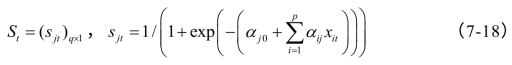
（4）进行各阈值和权系数调整：
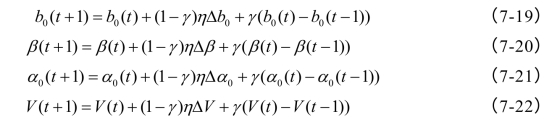
这里η为学习率，γ为动量因子。
采用学习率和动量因子自适应调整时，当总误差减小时，将权值和阈值的修正值乘以一个增量因子，同时可加入动量项，使其修正值增加；而当总误差增大时，减小修正值，而对于动量因子，则可令其为0，即修正值中不含动量项；当总误差不变时，则不改变学习率和动量因子。如下式：
这里kinc﹥1,kdec﹤1。
（5）同步骤（2），对于输入值Xt＝(x1t,x2t,…,xpt)′，按调整后的各阈值和权系数向输出层逐层计算输出估计值
，计算标准误差
，若标准误差小于给定的误差ε，则转至（6）；否则，转至（3），进行下一轮阈值和权系数的最值梯度法调整。
（6）输出各阈值和权系数的估计量，得到式（7-12）所示的BP神经网络方法的估计量。
在BP神经网络方法进行非线性函数逼近与参数估计时，当真实函数形式较为复杂时，上述算法需进一步改进。
关于神经网络隐层神经元个数的确定方法，主要有三种：（1）Fahlman与Lebiere（1990）提出的构造算法，其思想为先设计一个小规模网络，然后根据网络性能要求逐步增加隐节点或隐层，直至满足性能要求。（2）Ehud与Karninl（1990）、Erdogan等（1996）提出的修剪算法，其思想为先构造一个足够大的网络，训练收敛后删除网络中冗余参数并重新训练和测试网络。（3）GA遗传算法，而Kim与Cho（2008）则提出了进化算法，该方法具有很好的鲁棒性[1]（Robustness）和全局搜索能力，比较适合寻找最佳的网络结构或参数。
张昭昭等（2009）定义了神经网络连接权值的e指数信息熵，该熵克服了shannon熵固有的缺点，但与Shannon熵对不确定性的描述具有相同的效果。将其作为惩罚项引入神经网络学习的目标函数中训练神经网络，由于熵函数特有的属性，对神经网络中小的连接进行惩罚而对大的连接进行鼓励，从而使神经网络中小的权值迅速收敛到零值附近。通过删除零值附近的权连接进而达到简化神经网络结构的目的。但该法没有考虑动量项，并且对何时剪枝退出没有给出具体要求，使得MC仿真模拟显示容易过度剪枝，为此，本书改进了该算法，对隐层神经元的剪枝进行动态确定。具体算法思路如下：
张昭昭等（2009）定义的新信息熵为：
对于事件发生概率pi，有：
归一化的熵为：
这里C＝1/(e(1－1/n)－1)。那么，H*(pi)的取值范围是[0,1]。(www.xing528.com)
对于上述BP算法中输入层到中间层的连接权矩阵V＝(αij)p×q，以及中间层到输出层的连接权矩阵W＝(βk)q×1，分别令其权值概率为：
那么，网络权矩阵的输入层和输出层的权值信息熵为：
这里C1＝1/(e(1－1/pq)－1)，C2＝1/(e(1－1/q)－1)。
对输出层和中间层分别引入基于熵的惩罚项HO和HI，惩罚因子为λ，则在前述BP算法的步骤（3）中按最值梯度下降法加入两个调整项：
这里
和
这里
进一步，将步骤（4）中的权系数调整为：
如此，使得权重大的更大而权重小的更小，当W＝(βk)q×1中某连接点权重小于给定阈值则删除与该权重相对应的神经元，起到剪枝的作用。同时，为避免过度剪枝，引入剪枝算法的退出机制：当总误差项不再快速下降时，取惩罚因子λ＝0，信息熵不再对连接权起作用，隐层神经元个数不再改变，仍由前述BP算法完成相应函数逼近。
MC表明上述算法可以防止局部最小的陷阱，但收敛速度仍然很慢，其泛化能力也不强。基于此，本书重点研究Moller（1993）提出的一种快速LM（Lenberg-Marquardt）算法，该算法是一种利用标准的数值优化技术的快速算法，其特点是梯度下降法与高斯-牛顿法的结合，既有高斯-牛顿法的局部收敛性，又具有梯度下降法的全局特性。冯今朝等（2007）、黄忠明等（2009）MC仿真与实证研究表明，LM算法优于其他BP改进模型[2]。该算法的基本思路为：
（1）如前图5-1所描述的网络模型，将阈值β0、中间层到输出层的连接权矩阵W＝(βk)q×1、各中间层阈值αj0以及输入层到中间层的连接权矩阵V＝(αij)p×q组成一向量
初始化该向量，赋予[－1,1]间的随机数。
（2）对于输入值Xt＝(x1t,x2t,…,xpt)′，开始向输出层按式（7-12）逐层计算各神经元的输出：
（3）计算训练误差，总误差为：
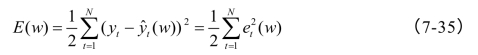
计算Jacobian矩阵：
这里n＝(p＋2)q ＋1，则高斯-牛顿法的各系数调整为：
LM算法为其一种改进形式：
这里μ﹥0为比例系数，In×n为单位矩阵。当μ＝0，则为高斯-牛顿法；若μ取值很大，则算法接近最值梯度下降法。LM算法利用了近似的二阶导数信息，因而比梯度下降法快得多。
（4）进行各阈值和权系数调整：
（5）同步骤（2），对于输入值Xt＝(x1t,x2t,…,xpt)′，按调整后的各阈值和权系数向输出层逐层计算输出估计值
，计算标准误差
，若标准误差小于给定的误差ε，则转至（6）；否则，转至（3），进行下一轮阈值和权系数的LM法调整。
（6）输出各阈值和权系数的估计量，得到式（7-12）所示的BP神经网络方法的估计量。
利用上法进行MC模拟会产生振荡，Moller（1993）的方法是在步骤（5）中加入一个判定步骤：若E(w(k＋1))﹤E(w(k))，则令μ＝μ/к(к﹥1)，回到步骤（2），否则不更新权值和阈值，令μ＝μк，重新计算Δw。
本书MC仿真研究发现，上述算法需对因子к进行调试，并且当要逼近的函数复杂度提高时，程序不稳定，并且收敛速度受初始值的影响。因此，提出另一种避免振荡的方法，即引入学习步长和动量项，将步骤（4）改为：
（4）*进行各阈值和权系数调整：
这里η为学习率，γ为动量因子。
MC仿真研究表明，上述改进算法的收敛速度在逼近难度不高的函数形式要稍慢于标准LM算法，但对难度高的函数形式则更稳健，即具有更好的鲁棒性。
例7-1 考察函数f(x)＝sin(2πx)＋sin(4πx)，x∈[0,1]，取样步长为0.01。应用BP-LM改进算法，神经元个数为6个，迭代1000次，逼近效果如图7-2所示：
图7-2 左边为拟合图，曲线为逼近值，点为函数值；右图为适应度变化图[3]
由图7-2可知，迭代200次的逼近精度就已经非常高，迭代1000次时的总平均误差则为：7.4979417e-005，这说明，LM算法远远优于普通BP算法，改进后的LM算法则可以避免局部最小的陷阱，从而具有很强的泛化能力。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
