非线性协整时间序列的非参数方法研究

在非线性非平稳时间序列的分布函数和非线性结构未知时，可以应用核密度函数与核回归的思想进行估计，局部核权最小二乘法则为一种估计非线性协整结构的非参数检验方法。

Nadaraya（1964）和Wat-son（1964）提出了非参数回归模型的核估计，其思想相当于将回归函数按局部零阶台劳展开的加权最小二乘估计。Stone（1977）和Cleve-land（1979）研究了回归函数局部线性台劳展开的核权最小二乘估计。Mach与Müller（1989）以及Chu与Mar-ron（1991）进一步研究表明：当解释变量是随机变量时，Nadaraya-Watson核估计的方差和局部线性回归估计的相同，但偏多了一项。Fan（1992，1993）以及Fan与Gijbels（1992）发现局部线性拟合不必进行边界修正，它在边界的偏差自动与内部的偏差有相同的阶，因而局部核权线性回归估计较N-W核估计有更好的性质。Ruppert和Wand（1994）将一元局部线性回归估计结果推广到多元情形。叶阿忠（2001）基于此局部线性回归原理提出局部核权最小二乘法，应用于检测我国商品进出口总额、差额和通货膨胀之间的非线性协整关系，表明该方法是有效的。

本书给出其多元局部核权最小二乘法的基本思路：

（1）假设时间序列X＝{x1t,x2t,…,xpt}与{yt}的非线性均衡方程存在，其非线性协整模型为：

这里{ut}为随机误差项，非线性函数f(∙)未知。

（2）对于样本(y1,X1)，(y2,X2)，…，(yN,X N)，设f(X)在X＝X0处的2阶偏导数存在，则先将f(X)在X＝X0处进行台劳线性展开：(www.xing528.com)

（3）对该局部线性模型应用核权最小二乘法进行局部拟合，也即最小化：

这里H为依赖于N的p×p正定矩阵；p元核函数K(∙)满足以及。

对核函数的讨论也可参见本书第5章5.1.2。对于确定的核函数，则当X0取Xt,t＝1,2,…,N，就可以得到f(Xt,θ)的估计，从而可以求得残差＝。对其可进行平稳性检验以确定原序列间是否具有非线性协整。

这里，窗宽的确定可使用Stone（1977）提出的交错鉴定方法（Cross Validation Method）。即对每个局部观察点X0＝Xi，首先在样本中剔除该观察点(Xi,yi)；其次，将剩下的N－1对观察点在X0＝Xi处进行局部核权回归，则得到的是常数项αt＝f(Xt)的估计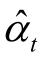；最后，通过比较平均拟合误差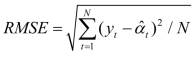的大小选择使平均拟合误差最小的窗宽。

局部核权最小二乘法和ACE法对于非线性结构的估计，其具体形式仍然是不确定的，其是否能完全析出序列间的非线性结构也没有理论保证，而神经网络法则可以在不知道非线性结构具体形式的前提下近似逼近该非线性函数，并且可以给出一个显性表达式，因此更具有现实应用性，本书重点加以讨论。