单位根与协整关系秩检验的研究成果

1.协整关系存在性检验

首先，本书应用单位根的秩检验统计量RDF，λT(uni)以及λT(INS)对各股指序列进行单位根检验，注意到严格单调递增变换不改变秩序，故只需对原始数据进行检验，结果见表6-12。

表6-12　单位根的RDF，λT(uni)以及λT(INS)检验结果

续表

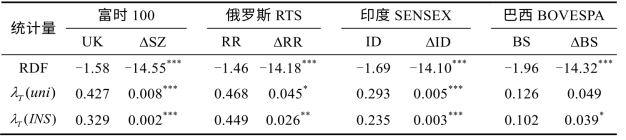
注：各检验变量序列的第一列为水平检验值，第二列为一阶差分后的检验值。秩检验考虑到变量数列中数据相等的情形影响秩序，对秩检验程序进行了修正，其结果与未检验前是一致的，故未报告。*，**，***分别为10%，5%，1%显著性水平下拒绝单位根的原假设。

各秩检验表明，各指数序列均在1%显著性水平下通过RDF检验为I（1）序列，对于其余两秩检验统计量，除指数BS外都为一阶单位根序列。对于指数BS，λT(INS)也表明其为一阶单位根序列，逆得分秩λT(uni)则在 10% 的显著性水平下没有拒绝单位根的原假设，究其原因，本书发现，受股指异常值影响明显，在去掉两个异常值后，逆得分秩λT(uni)值在10%的显著性水平下显著，逆正态得分秩λT(INS)值在5%的显著性水平下显著。秩检验结果显示，原始序列及其严格单调变换后的序列均为一阶差分平稳。

其次，本书进一步考察上证股指与各国股指的协整关系，利用非线性协整关系的秩检验方法，检验结果见表6-13至6-16。

对于两股指的情形，很强的证据（各检验统计量均在5%显著性水平以上拒绝原假设）支持上证综指（SZ）与巴西BOVESPA指数（BS）之间存在一个协整关系。较弱的证据表明，（SZ，GM），（SZ，RR）与（SZ，ID）可能存在协整关系。其中，注意到（SZ，ID）虽然调整前的各检验秩均认为其存在协整关系，但是考虑相关性后的各秩检验统计量均不显著，因此本书只能推断其可能存在协整关系。

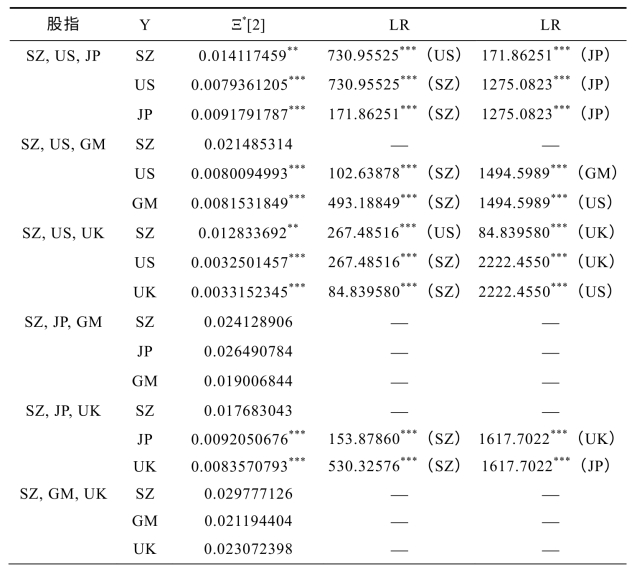
对于三股指及以上的情形，к与ξ统计量不再适用，本书使用双侧检验统计量Ξ[k]，考虑到可能存在的相关性，使用调整后的Ξ*[k]统计量。对于多变量情形（k≥2），由式（6-9），需要R(Y)^[4]对其他各股指的秩进行OLS回归，利用似然比LR作为辅助工具来确定各回归系数是否显著。由表6-14可知，对于取不同的股指的秩作为被解释变量，Ξ*[2]的值至少有一个以上1%的显著性水平支持（SZ，US，JP），（SZ，US，GM），（SZ，US，UK），（SZ，JP，UK）以及（SZ，ID，BS）存在协整关系，5%的显著性水平有一个Ξ*[2]的值支持（SZ，RR，ID）与（SZ，RR，BS）股指组合存在协整关系，Ξ*[2]的值显示只有两个组合不存在协整关系。

表6-13　非线性协整关系的秩方法检验结果

注：由于秩差分系数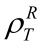都较小，故本书没有报告统计量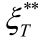和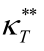的值。**，***分别为5%，1%显著性水平下拒绝不存在协整关系的原假设。所用临界值来自Breitung（2001）中表1。统计量Ξ*[1]检验的被解释变量Y取SZ，SZ作为解释变量的检验结论与前述一致，故未报告。

表6-14　非线性协整关系的双侧检验Ξ*[2]的检验结果

续表

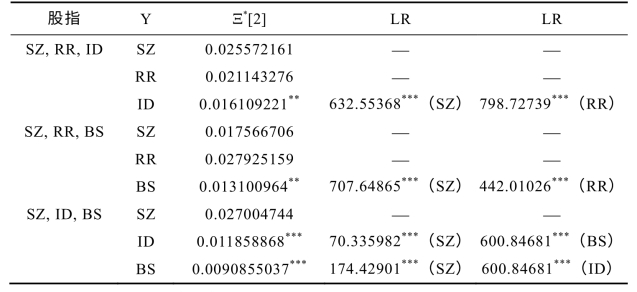
注：检验统计量来自式（6-10），检验的被解变量为R(Y)。**，***分别为5%，1%显著性水平下拒绝不存在协整关系的原假设。所用临界值来自Breitung（2001）中表1。

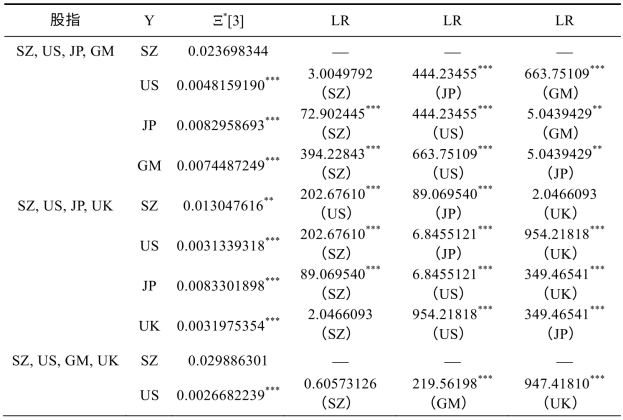
对于四股指的情形，虽然R（SZ）为被解释变量时只有一个股指组合（SZ，US，JP，UK）在5%的显著性水平下存在协整关系，但取其他股指的秩为被解释变量时，至少有一个以上的Ξ*[3]值在1%的显著性水平下表明，表6-15中各四股指组合均存在协整关系。

表6-15　非线性协整关系的双侧检验Ξ*[3]的检验结果

续表

注：同表6-14.(www.xing528.com)

对于五股指组合（SZ，US，UK，GM，JP），双侧检验Ξ*[4]的检验结果表明，虽然R(SZ)作为被解释变量并不存在协整关系，但其余情形均在1%的显著性水平下支持组合存在协整关系。

表6-16　非线性协整关系的双侧检验Ξ*[4]的检验结果

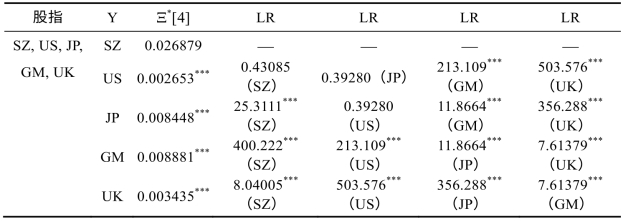
注：同表6-14.

2.协整关系存在非线性的检验

上述秩检验检测到的股指组合的协整关系是线性的还是非线性的需进一步进行检验。对于表6-16中的结果，应用检验统计量TR2检测是否为非线性协整关系，考虑到序列相关性，由式（6-11）、（6-12），有必要确定滞后期，本书使用Ljung-Box Q^[5]统计量在5%的显著性水平下进行确定。检验结果见表6-17至6-20。

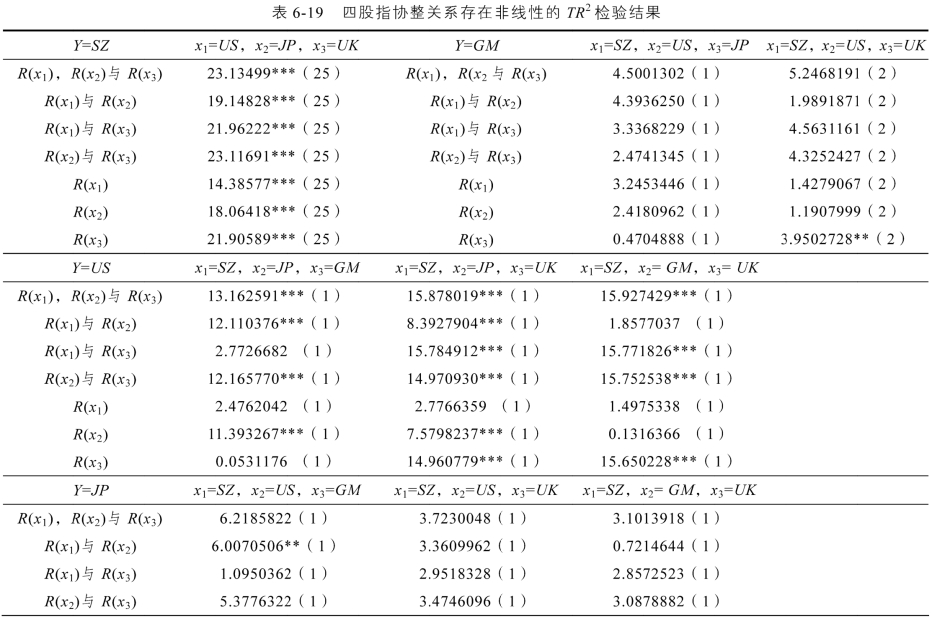
对于两股指的情形，由表6-17，TR2检验结果表明，（SZ，BS）的协整关系在5%的显著性水平下，存在非线性关系；对于其他股指，组合（SZ，GM），（SZ，RR）与（SZ，ID）的TR2检验均不显著，因此可能存在的协整关系为线性协整关系。

表6-17　两股指协整关系存在非线性的TR2检验结果

注：检验式基于公式（6-11）、（6-12）。**，***分别为5%，1%显著性水平下拒绝协整关系是线性的原假设。检验的被解释变量为Y，所用临界值来自Breitung（2001）中表1。滞后期由Ljung-Box Q统计量所有值均在5%内确定。

对于三股指的情形，TR2检验结果表明，股指组合（SZ，US，JP），（SZ，US，GM），（SZ，US，UK）与（SZ，JP，UK）的协整关系均在1%的显著性水平下存在非线性协整关系。尽管上述组合中可能有一个或两个股指秩序不显著（即不是非线性产生的来源），但秩序组合中只要有一个显著，则认为检验的股指组合的协整关系存在非线性。TR2的值显示，对于“金砖五国”含上证综指的三股指组合中（SZ，ID，RR）和（SZ，RR，BS）为线性的，而（SZ，ID，BS）虽然单个秩序R（SZ）、R（BS）不显著，但两者的组合却在5%显著性水平下显著，故认为其协整关系可能是非线性的。

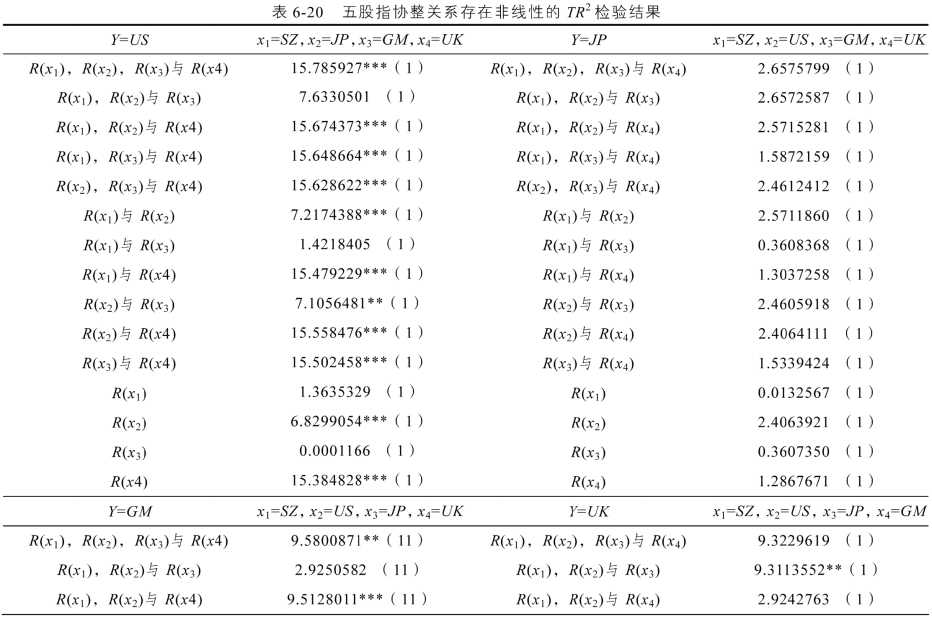
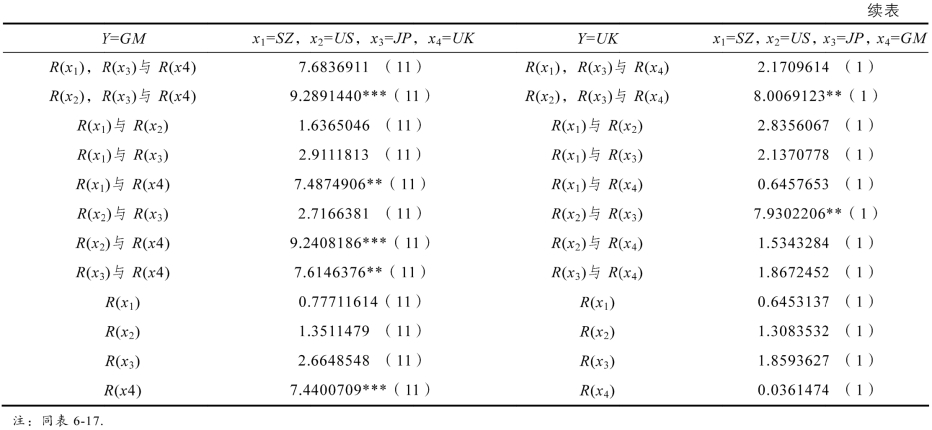
对于四股指的情形，由表6-19，TR2检验结果表明，在1%的显著性水平下支持（SZ，US，JP，UK）存在非线性协整关系，并且各股指都为非线性产生的来源，结合前述分析，股指UK的线性部分不显著，但非线性部分显著，因此本书认为股指组合（SZ，US，JP，UK）存在非线性协整关系。股指组合（SZ，US，JP，GM）和（SZ，JP，GM，UK）中有一种情形TR2的值在1%显著性水平下支持存在非线性。对于股指组合（SZ，US，GM，UK），虽然整体表明存在非线性，但是总有一个股指的线性部分与非线性部分同时不显著，从而认为可能存在非线性协整关系。最后，股指组合（SZ，RR，ID，BS）的各TR2值均表明不存在非线性，本书认为股指组合（SZ，RR，ID，BS）是线性的协整关系。

对于五股指的情形，由表6-20，股指组合（SZ，US，JP，GM，UK）有两种情形TR2的值在1%显著性水平下支持协整关系为非线性的，表6-20中第二种情形即被解释变量为JP，结果不支持存在非线性，结合表6-16的结果，R(US)不显著，则组合退化为四股指的组合。综上分析，本书认为，五股指组合（SZ，US，JP，GM，UK）存在非线性协整关系。

综合上述分析，对于中国上证综指与国际上其他国家的股票指数间的非线性协整关系的秩检验方法分析结果，存在线性（或非线性）协整关系的股指组合见表6-21。

表6-21　中国上证综指与国际股市组合的非线性协整关系秩检验结果

由表6-21的结果，与Johansen协整检验相比较，本书可以将其分为四类，第一类情形为Johansen协整检验没有报告而秩检验表明存在协整关系，第二类为两种检验结论有冲突的情形，第三类为Johansen协整检验不能确定协整关系为线性或非线性而秩检验则可确定的情形，第四类为两者检验结论一致。对于情形2，（SZ，BS）仅有较弱的秩检验证据表明协整关系存在非线性，而组合（SZ，JP，UK）与（SZ，US，JP，UK）则有较强的秩检验证据表明协整关系存在非线性。

检验结果还表明，利用取对数后的数据进行Johansen协整检验可以探测部分组合的非线性关系，但由秩检验的结果表明，至少有三种股指组合{（SZ，BS），（SZ，US，GM）与（SZ，JP，UK）}的非线性关系利用取对数的方法是不能发现的，即股指之间的协整关系为其他非线性关系，需要利用其他的单调变换来实现。

总之，可以发现，秩检验能够检测到更多的线性和非线性协整关系，从而给我们提供了较多的变量间存在线性或非线性协整关系的信息。