非线性协整时间序列的非参数方法与应用

进行统计检验，不仅要有检验统计量，而且还要给出检验统计量的分布和各种分位数值，即各种显著性水平下的临界值。由于协整秩检验统计量并不服从标准分布，所以其分布与检验临界值只能通过Monte Carlo仿真模拟和响应面函数来实现。

6.2.3.1　非线性协整秩检验的临界值表

使用Monte Carlo方法，利用Gauss编程，对各种秩统计量的取值进行模拟计算，可得到各统计量的频率分布和各种分位数值。

1.两变量情形

设两个随机变量y1t＝f1(x1t)和y2t＝f2(x2t)都是I(1)序列，其中fi(∙)为单调递增函数。按yit＝yit－1＋εt，εt～N(0,1)，i＝1,2，重复生成10000个样本容量为T的随机游走序列。由于任何单调递增变换都不改变序列的秩，故可以应用yit序列的秩代替xit序列的秩进行计算。对每个样本分别计算统计量к，к*，к**，ξ，ξ*，ξ**，Ξ[1]与Ξ*[1]的值，就可得到这些统计量的频率分布。图6-1给出了T=100时各秩检验统计量的频率分布。

图6-1　T=100时，秩检验统计量к，к*，к**，Ξ[1]（上排）与ξ，ξ*，ξ**，Ξ*[1]（下排）频率分布

由图6-1可知，未调整前的秩统计量к，ξ与Ξ[1]，其分布形态没有呈现明显的集中趋势，к左偏，但较ξ与Ξ[1]稳健；调整后的秩统计量к*，к**，ξ*，ξ**与Ξ*[1]，则呈现较明显的集中趋势，具有更好的统计规律，从形态上看，к*，к**呈现钟形分布，而ξ*，ξ**与Ξ*[1]右偏。若考虑到检验的拒绝域位于频率分布的左侧，则к*，к**更为稳健。

由各个秩检验统计量的频率分布，给定显著性水平，就可确定出其临界值，如表6-1和表6-2所示。

表6-1　秩检验统计量к，ξ与Ξ[1]的临界值

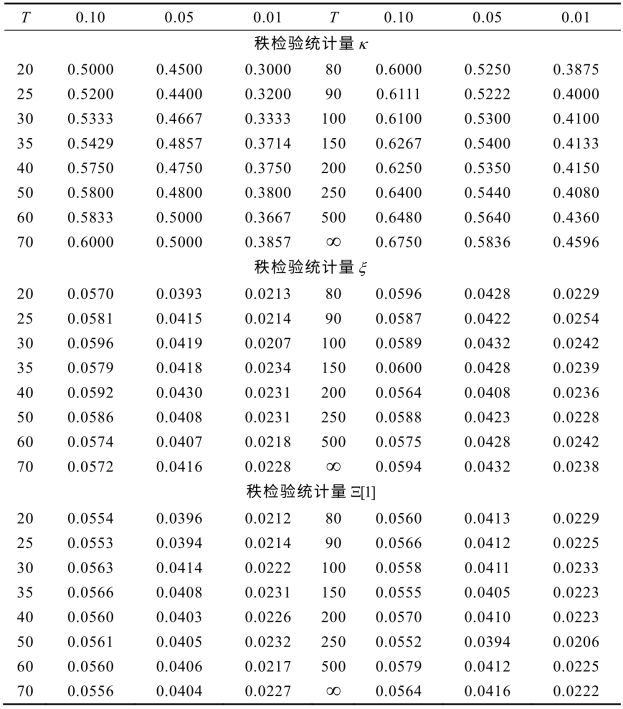
表6-2　调整的秩检验统计量к*，ξ*，к**，ξ**与Ξ[1]*的临界值

续表

2.多变量情形

对于多变量的情形，检验只能使用秩统计量Ξ[k]和Ξ[k]*。设k＋1个随机变量yit＝fi(xit)都是I(1)序列，fi(∙)为单调递增函数，仍按yit＝yit－1＋εt且εt～N(0,1)生成数据，并计算秩次，重复10000次分别计算秩检验统计量Ξ[k]和Ξ[k]*的值，就得到各自的频率分布。图6-2给出了样本容量T=100且k=2和6时两秩统计量的频率分布。

图6-2　T=100时，秩检验统计量Ξ[2]，Ξ*[2]，Ξ[6]与Ξ*[6]频率分布

由图6-2可见，随着序列数k的增加，Ξ[k]*的频数分布形态基本相同，但右偏程度降低；对于Ξ[k]，则集中趋势明显加强。由于多序列协整检验的解释变量通常彼此相关，因而实际应用中多只报告调整的Ξ[k]*值，故而本书后继响应面函数研究仅对Ξ[k]*展开。

在给定的显著性水平之下，由模拟得出的频率分布，就可分别计算出秩检验统计量Ξ[k]和Ξ[k]*的各个临界值，如表6-3所示。

表6-3　调整的秩检验统计量Ξ[k]*的临界值(www.xing528.com)

续表

续表

6.2.3.2　检验统计量临界值的响应面函数

研究检验统计量临界值的响应面函数就是要给出检验统计量的临界值随样本容量变化而变化的多项式回归方程，以便能计算出任一样本容量下检验统计量的临界值。MacKinnon等（1991，1996，1999，2002）曾给出了多种线性协整检验如Engle-Granger检验和Johansen检验等检验统计量的临界值的响应面函数；贺京同、李峰（2007）则给出了单位根检验PT统计量的响应面函数。本书借鉴了这些研究的思路。

下面给出各秩检验统计量的渐近分布图。利用MC模拟，取样本容量T分别为50，100，200，500，首先给出两序列的各秩检验统计量的累积分布函数，如图6-3所示。

图6-3　T=50，100，200，500时，秩检验统计量к，к*，к**，Ξ[1]（上）与ξ，ξ*，ξ**，Ξ*[1]（下）的累积分布图

其次给出多序列的各双侧秩检验统计量的累积分布函数，如图6-4所示。

图6-4　T=50，100，200，500时，秩检验统计量Ξ[k]（上排）与Ξ*[k]（下排），k＝2,3,4,5的累积分布图

为了建立协整秩检验统计量的临界值随样本容量变化而变化的多项式方程，根据表6-1至6-3给出的检验统计量的一系列有限样本的频率分布和其渐近分布的分位数值，可绘出各秩检验统计量分别在10%，5%和1%三种不同显著性水平之下的临界值随样本容量T的变化曲线，如图6-5所示。观察这些变化曲线，就可发现和掌握其变化规律。

图6-5　各秩检验统计量的临界值在不同显著性水平α＝0.10,0.05,0.01下随样本容量的变化图（各秩检验统计量的顺次为к，к*，к**，ξ，ξ*，ξ**，Ξ*[1]，Ξ*[2]，Ξ*[3]，Ξ*[4]，Ξ*[5]和Ξ*[6]）

由图6-5可见，秩统计量к的临界值随T值的增加而增加，当T值较大时，增加的速度渐缓，而调整的к*，к**值基本没有变化；统计量ξ值并不随T值的增加而变化；其余秩检验统计量则呈现随T值的增加而渐近递减的趋势。根据各个秩检验统计量的临界值的变化趋势，可构造出相应的多项式趋势模型，即响应面函数，然后进行拟合估计，即可得到各个近似计算公式。这些响应面函数及其估计结果都列在表6-4之中。