1.基于一般累积分布函数(Cumulative Distribution Function,CDF)的逆得分秩
实际应用时,由于本书很难保证随机误差项是正态的,因此,本书进一步将标准正态分布函数加以推广。考虑到随机步游的误差为独立同分布,其分布为一般单峰分布函数FT(y),方差为σ2,令Rt为rt的变换为:
式(5-21)中的分布函数F(∙)可以由误差的经验分布函数![]() 得到,记
得到,记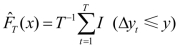 。由于
。由于![]() 逐点收敛于误差分布F(x),变换
逐点收敛于误差分布F(x),变换![]() 表示一个与Δyt有相同分布性质的序列,从而可得到一个更为广泛的秩检验统计量——逆得分秩统计量为:
表示一个与Δyt有相同分布性质的序列,从而可得到一个更为广泛的秩检验统计量——逆得分秩统计量为:
其渐近分布推导如下:
设随机变量X的分布函数为F(x),定义:F-1(y)=inf{x:F(x)≥y},0≤y≤1。
定理5-2 令{ε1,…,εT}为独立同分布序列,σ2为εi的方差,在![]() 条件下,当T→∞时,有:
条件下,当T→∞时,有:
证明 令![]() ,令ξt,T为独立随机序列,满足:
,令ξt,T为独立随机序列,满足:
则规范秩向量(Q1,T,…,QT,T)与随机向量(ξ1,T,…,ξT,T)在条件![]() 下有相同的渐近分布。因为ξt,T与ξs,T(t≠s)相等的概率渐近可忽略,又ξ1,T,…,ξT,T渐近趋于均匀分布U(-0.5,0.5),故而Q1,T,…,QT,T亦渐近趋于均匀分布U(-0.5,0.5)。
下有相同的渐近分布。因为ξt,T与ξs,T(t≠s)相等的概率渐近可忽略,又ξ1,T,…,ξT,T渐近趋于均匀分布U(-0.5,0.5),故而Q1,T,…,QT,T亦渐近趋于均匀分布U(-0.5,0.5)。
由此,在条件![]() 渐近趋于均匀分布U(0,1)。由引理5-1,Rt渐近服从分布F(x)。注意到独立性与条件
渐近趋于均匀分布U(0,1)。由引理5-1,Rt渐近服从分布F(x)。注意到独立性与条件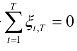 ,有:
,有:
最后由此可得:
证毕。
上述推导与前述正态分布的情形基本一样,即除去方差σ2,一般单峰分布的逆得分秩统计量的渐近分布与标准正态分布序列的逆得分秩统计量的渐近分布是一致的。这可以从另一方面利用Box-Cox(1964)提出的Box-Cox变换[3]加以解释,即一般单峰分布变量可以通过Box-Cox变换转变为正态性变量,由于Box-Cox变换要求变量为正,李选举(2000)指出,当不满足该条件时则做一平移即可。由此可见,对时间序列进行上述变换后为严格单调的,而单调变换不改变时间序列的秩。基于此,也可以得出:除去方差σ2,一般单峰分布的逆得分秩统计量的渐近分布与标准正态分布序列的逆得分秩统计量的渐近分布是一致的结论。
2.基于自助法(Bootstrap)的逆得分秩自适应检验
对于真实数据序列,其随机误差项的分布未知,直接应用秩检验则会降低其检验功效,而检验水平扭曲增大,进而影响检验结果的可靠性。Efron(1979)提出了基于残差的重抽样方法,计算机仿真表明,其具有优良的稳健性特征;Mantalos(2000)、Shukur和Mantalos(2000)仿真研究表明,应用这种方法能够使检验更为接近预先给定的水平。仿真结果还表明,在小样本或中等样本的情形下,Bootstrap方法比通常Wald检验以及LR似然比检验的效率更高。本书采用自助法对序列残差进行重抽样,进一步计算逆得分秩,并且通过MC仿真模拟给出其临界值,并进行序列的单位根检验。其基本步骤为:
(1)计算式(5-10)的残差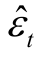 ,t=1,2,…,T 。(https://www.xing528.com)
,t=1,2,…,T 。(https://www.xing528.com)
(2)对于残差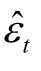 ,t=1,2,…,T,估计εt的经验分布:
,t=1,2,…,T,估计εt的经验分布: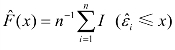 。
。
(3)生成
Bootstrap数据序列: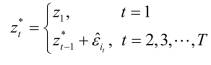 ,其中it是从{1,2,…,T-1}中随机抽取的。
,其中it是从{1,2,…,T-1}中随机抽取的。
(4)利用式(5-21)、(5-22)计算逆得分秩,并且,重复步骤(3)、(4)计算逆得分秩的临界值。
(5)对原序列计算逆得分秩并与临界值比较确定接受或拒绝原假设。
3.基于残差的块形自助法(Residual-based Block Bootstrap,RBB法)的单位根逆得分秩自适应检验
在单位根检验中,考虑到经济数据时间序列存在一定的相依结构,Künsch、Liu和Singh(1992)独立提出了块结构的Bootstrap 方法。Paparoditis和Politis(2003)在单位根检验中提出基于残差的块形自助法(Residual-based Block Bootstrap,RBB法),该方法是对序列模型的OLS估计残差进行再抽样。Paparoditis Politis(2003)用自助泛函中心极限定理(Bootstrap Functional Limit Theorem)对RBB法统计量和ADF统计量的极限分布进行了比较研究,认为,当样本趋于无穷大和一些正则条件下,RBB法统计量与ADF统计量具有相同的极限分布。另外,Paparoditis和Politis(2003)通过MC仿真研究发现,RBB法比ADF法具有较小的检验水平扭曲,并且也具有比ADF法较高的检验势。RBB法的良好性质使其可应用于非对称单位根检验,国内学者刘汉中(2008)对其进行了研究,得到了很好的MC仿真模拟效果。对于实际序列,本书则考虑利用基于改进的RBB法对序列残差进行重抽样,进一步计算逆得分秩,并且通过MC仿真模拟给出其临界值,并进行序列的单位根检验。
改进的RBB法的基本步骤如下:
(1)计算式(5-10)的残差![]() ,t=1,2,…,T 。
,t=1,2,…,T 。
(2)中心化残差序列,其中b为小于样本容量n的正整数:
(3)对于残差![]() ,t=1,2,…,T,估计εt的经验分布:
,t=1,2,…,T,估计εt的经验分布:![]() 。
。
(4)生成![]() Bootstrap数据序列:
Bootstrap数据序列: ,其中,k=[(n-1)/b],l=kb+1,m=[(t-2)/b],s=t-mb-1,且i0,i1,…,ik-1是从{1,2,…,n-b}中随机抽取的;[∙]是不大于括号中数字的最大整数。
,其中,k=[(n-1)/b],l=kb+1,m=[(t-2)/b],s=t-mb-1,且i0,i1,…,ik-1是从{1,2,…,n-b}中随机抽取的;[∙]是不大于括号中数字的最大整数。
(5)利用式(5-21)、(5-22)计算逆得分秩,并且,重复步骤(4)、(5)计算逆得分秩的临界值。
(6)对原序列计算逆得分秩并与临界值比较确定接受或拒绝原假设。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




