非参数方法及其应用研究：秩检验方法（RankTest）

Granger and Hallman（1991）是最早提出单位根的秩检验思想的，他们基于DF检验t统计量提出了相对应的RDF（Ranked Dickey-Fuller）检验。其思想为：首先对原始序列及其相应的秩序列分别进行ADF检验和RADF检验，然后比较上述两种检验的结果，如果函数f是线性的，则两种检验的结果相同；如果函数f是非线性的，则原始序列的ADF检验将会拒绝零假设而RADF检验则不会拒绝原假设（单调变换不影响原始时间序列的秩次）。Campbell and Dufour（1995）对简单随机游走模型的研究发现，在强白噪声的假设下，可以应用Welcoxon检验，其对变换的分布影响是不变的。Breitung和Gouriéroux（1997）系统研究了前述秩检验方法，他们基于Schmidt and Phillips（1992）给出的得分统计量提出了相应的秩得分检验量λT(uni)，并推导了其分布，然后进一步讨论了改进的“逆正态得分（Inverse Normal Score）”变换的版本λT(INS)。Monte Carlo模拟表明，秩检验的小样本性质，在线性及正态性相关假设下，其功效稍差于常规检验，但较之更稳健；而对于非线性情形，则大大优于传统检验。因此，我们认为，对于非线性时间序列过程，秩检验是一个很好的工具。

5.2.1.1　RDF检验

设

其原假设为：H0＝{∃h(∙)为单调函数，εt～i.i.d:h(yt)＝h(yt－1)＋εt}；备择假设为：H1＝{∃h(∙)为单调函数，，εt～i.i.d:h(yt)＝αh(yt－1)＋εt}。

令，将其进行均值调整或者忽略回归常数，那么相对于传统DF检验的RDF检验统计量如下：

其中。

参数DF检验是基于事实：

其中，0≤a≤1，W(a)为[0,1]上的布朗运动。

然而，秩序列的渐近分布并非如此，注意到单调变换不改变秩次，Breitung和Gouriéroux（1997）证明：当T→∞时，秩序列T－1r[aT],T⇒aR1＋(1－a)R2，其中R1与R2为两个具有反正弦分布的独立随机变量（见Breitung和Gouriéroux，1997），从而利用该渐近分布性质可进一步推导RDF检验统计量的分布和性质。考虑到其复杂性，可利用Monte Carlo模拟。

通过分析和Monte Carlo模拟，Breitung和Gouriéroux（1997）发现，对于有限样本，RDF检验的实际水平依赖于误差分布，对于大样本，虽然其渐近分布独立于误差分布，但却会过度地拒绝原假设。并且，RDF检验也难以扩展到有漂移和相关误差情形的随机游走过程。

5.2.1.2　得分秩检验

令{xt}为观测到的时间序列，yt＝f(xt)是观测序列{xt}的单调非线性变换，但函数形式f(∙)未知，所以不能直接对变换后的序列{yt}进行检验。为了得到一个不受f(∙)的形式选择影响的单位根检验，基于Schmidt 和 Phillips（1992）的得分检验原理，Breitung和Gouriéroux（1997）提出了如下的秩检验方法。

原假设为＝{存在强白噪声εt，满足：Δyt＝εt}。

令，记rt为观测序列差分的归一化秩，即：，其中T为样本容量。检验统计量为：

这是得分型秩检验统计量的一个归一化版本，其渐近分布为，其中为[0,1]上的布朗桥。

5.2.1.3　逆正态得分秩检验

对于原假设，Breitung和Gouriéroux（1997）还提出了另一个秩检验统计量的版本，即基于“逆正态得分（Inverse Normal Score）”变换的版本。当随机游走的误差满足高斯白噪声序列分布，则令Rt为rt的INS变换，即

式中Φ(∙)是标准正态分布函数。秩检验统计量的INS版本为：

其渐近分布推导如下：

设随机变量X的分布函数为F(x)，定义：F－1(y)＝inf{x:F(x)≥y}，0≤y≤1。

引理5-1　设随机变量U服从(0,1)上的均匀分布，则X＝F－1(U)的分布函数为F(x)。

证明　P(X≤x)＝P(F－1(U)≤x)＝P(U≤F(x))＝F(x)。证毕。

定理5-1　令{ε1,…,εT}为独立同分布序列，在条件下，当T→∞，有：

证明　令，令ξt,T为独立随机序列，满足：

则规范秩向量(Q1,T,…,QT,T)与随机向量(ξ1,T,…,ξT,T)在条件下有相同的渐近分布。因为ξt,T与ξs,T(t≠s)的概率相等渐近可忽略，又ξ1,T,…,ξT,T渐近趋于均匀分布U(－0.5,0.5)，故而Q1,T,…,QT,T亦渐近趋于均匀分布U(－0.5,0.5)。

由此，在条件下，Q1,T＋0.5,…,QT,T＋0.5渐近趋于均匀分布U(0,1)，由引理5-1，Rt渐近服从标准正态分布，注意到独立性与条件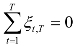，有：

最后由此可得：

证毕。

5.2.1.4　Monte Carlo仿真模拟

1.检验临界值表

为了给出各种秩检验的临界值表，可以利用Gauss编程，通过Monte Carlo模拟得到。记zt＝h(yt)，对于模型：

在存在单位根的原假设下，b = 1，备择假设为b < 1。为了简便，按zt＝yt，εt～N(0,1)，样本规模T，重复100000次生成随机游走数据。以T = 100为例，RDF统计量tα、得分秩检验统计量λT(uni)以及逆正态得分秩检验统计量λT(INS)的频率分布如图5-1所示。

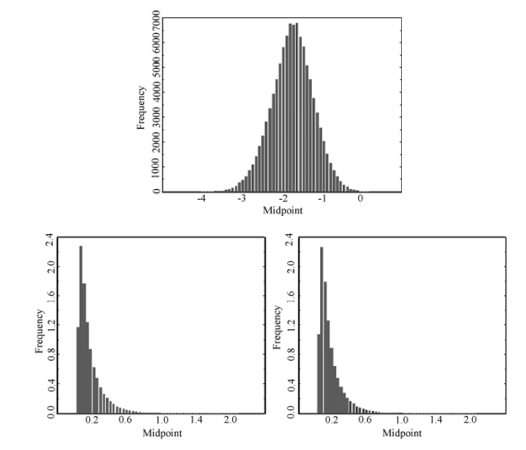
图5-1　随机游走在T=100时，秩统计量tα,λT(uni),λT(INS)的频率分布

其临界值如表5-1所示。

表5-1　三种秩检验的临界值

注：对于不同样本量T，其临界值响应函数由回归模型确定。（其中，标准误差：RDF不超过0.02，λT(uni)与λT(INS)不超过0.000195。）

上述三个秩统计量在不同水平下的临界值随样本量T的变化如图5-2所示：

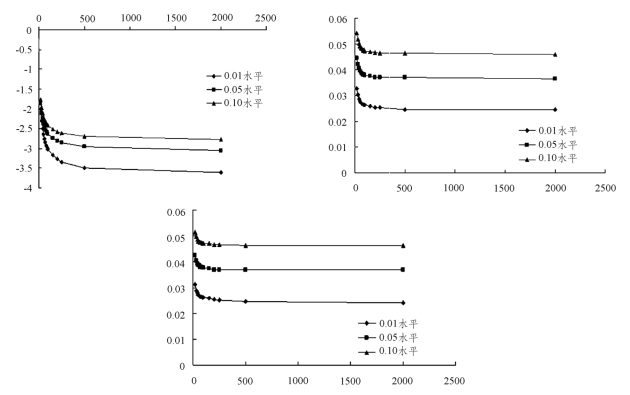
图5-2　秩统计量tα,λT(uni),λT(INS)在显著性水平0.01，0.05，0.10随样本量T的变化图(www.xing528.com)

由图5-2可看出，RDF统计量的分布与DF统计量相似，在正态假设下，秩得分统计量λT(uni)与逆正态得分秩检验统计量λT(INS)的分布形态相似。由图5-2还可看出，RDF统计量，对于小样本，较λT(uni),λT(INS)更敏感；而对于大样本，其值变化也相应较大。

2.检验功效及其比较

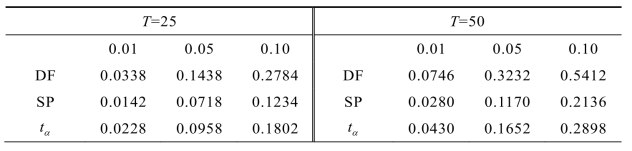
为了考察各种秩检验统计量的检验效果，给定备择假设分别为近单位根序列（b = 0.9）和白噪声序列（b = 0）两种情形，并分别给定样本量T = 25,50,100,500，各分别模拟5000次。在显著性水平分别为α＝0.01,0.05,0.10之下，得到DF检验、SP（Schmidt and Phillips）检验以及上述三种秩检验的功效，如表5-2和5-3所示。

表5-2　各检验在不同显著性水平下近单位根序列的功效值（Power）b=0.9

续表

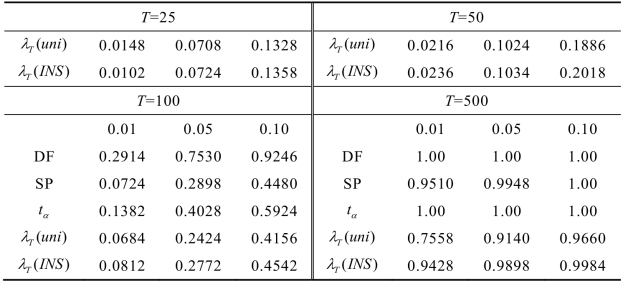
表5-3　各检验在不同显著性水平下白噪声序列的功效值（Power）

由表5-2可看出，对于随机误差为正态分布条件下的近单位根序列，在小样本情形下，各检验的功效都非常低，DF检验明显优于其他检验；只有在样本充分大（T = 500）时，各检验统计量才有很好的检验功效。RDF统计量的功效较另两个秩检验统计量高，秩得分统计量劣于逆正态得分统计量。

由表5-3可看出，对于白噪声序列，单位根的参数检验统计量要优于秩检验统计量，RDF统计量的功效较另两个秩检验统计量高且近于参数统计量。秩得分统计量劣于逆正态得分统计量，而两者的小样本功效很低，对于T = 25的情形，仅RDF统计量基本可行。

3.不同误差分布下的样本性质

用χ2(1)与t(2)分布分别代表有偏和厚尾误差分布。以T = 100为例，注意到χ2(1)分布取值为正数，RDF统计量总为一个只与T有关的固定值，故不适合。在不同误差分布下，各单位根检验的功效与水平如表5-4所示。

表5-4　各检验在不同显著性水平单整分布下的功效值与水平值（T=100）

注：仿真模拟检验序列，检验功效取zt＝εt,t＝1,2,…,T，εt～χ2(2),t(2)，检验水平取zt＝zt＋εt,t＝1,2,…,T，εt～χ2(2),t (2)，模拟重复5000次。

对于T = 100的情形，在0.05显著性水平下除得分秩检验稍显不足外，各检验的功效和水平都是不错的，DF检验对有偏和厚尾分布都有很高的功效和较低的水平，秩得分统计量劣于逆正态得分统计量。

对于时间序列中出现异常值（或离群值）的情形，考虑单点异常值（Additive Outlier，AO）和创新离群（Innovative Outlier，IO），假设异常发生的时点为T/2，异常值的大小为5σ。对于式（5-20）中系数b分别为1.0、0.9、0.8的三种不同取值，各种检验的拒绝频率如表5-5所示。

表5-5　各检验在显著性水平为0.05，不同系数b下拒绝频率（T=100）

由表5-5可看出，无论是单点异常值（AO），还是创新异常值（IO），秩检验统计量的检验水平相当稳健，而传统的DF检验和SP检验在样本较小且存在单点异常值时，其检验水平则会出现扭曲，因此秩检验优于传统检验。然而，对于近单位根的检验，当样本较小时，秩检验的功效却低于DF检验。

4.非线性变换的样本性质

现设序列由以下模型生成：

其中单调变换函数分别为：

以T = 100为例，在显著性水平为0.05下的拒绝频率如表5-6所示。

表5-6　各检验在显著性水平为0.05下的检测检验水平（T=100，500）

注：仿真模拟检验序列取yt＝h－1(zt)，zt＝zt－1＋εt,t＝1,2,…,T ,εt～N(0,1)，模拟重复5000次。

由表5-6的模拟结果可知，传统单位根检验受单调变换函数形式的影响非常明显，特别是对数变换，在5%的名义检验水平之下，却有75%以上的频率拒绝存在单位根的原假设，表明存在严重的检验水平扭曲。但是，秩检验的实际检验水平却与名义水平很接近，表明秩检验对于非线性变换相当稳健。其原因是传统单位根检验是基于线性随机游走的设定，而单调非线性变换并不影响秩检验的结果。因此，对于时间序列中的非线性变换检测，秩检验具有明显的优势。

5.具有随机误差项序列相关的场合

Schwert（1989）、Agiakloglou & Newbold（1992）的研究表明，如果随机误差项由近单位根的MA过程生成，参数单位根检验的效果很差，此时PP检验被应用于误差项存在自相关的情形，然而其检验水平却有巨大的偏误。为了考察这种状况下各种秩检验的效果，假设模型zt＝bzt－1＋εt中的误差项为MA(1)过程，有εt＝ut－βut－1，然后使用Monte Carlo模拟，得到三种秩检验和传统参数PP检验以及SP检验的拒绝频率，如表5-7和表5-8所示。其中，对于PP检验的滞后截断，参考Newey and West（1987），取q＝o(T1/4)。

表5-7　各检验在显著性水平为0.05下对MA(1)的拒绝频率（T=100）

续表

注：仿真模拟检验序列取zt＝bzt－1＋εt,t＝1,2,…,T ,εt＝ut－βut－1,uti.i.d～N(0,1)，模拟重复5000次。

表5-8　各检验在显著性水平为0.05下对MA(1)的拒绝频率（T=500）

注：仿真模拟检验序列取zt＝bzt－1＋εt,t＝1,2,…,T ,εt＝ut－βut－1,uti.i.d～N(0,1)，模拟重复5000次。

表5-7的结果表明，对于T =100的情形，PP检验在处理具有随机误差项序列的相关问题上要优于其他检验，但当β≥0.6时，PP检验的实际检验水平有较为严重的偏差，而秩检验的检验效果则与参数检验SP相当。对于b＝0.8的情形，PP检验功效明显优于SP检验及秩检验，这一结果与Breitung和Gouriéroux（1997）的研究结果有些不一致，而对于秩检验值则基本一致。

当T = 500时，如表5-8所示，PP检验对于误差项具有序列相关的情形仍然存在明显的优势，但当β≥0.4时，其实际检验水平就出现了较为严重的偏差。对于b＝0.8，秩检验基本不逊于传统检验统计量。可见，当样本量充分大时，序列相关的情形应用秩检验也是可行的，特别是对于正的序列相关，秩检验是可以胜任的。

6.主要结论

由以上分析，对于非平稳时间序列的检验，本书有如下结论：

（1）对于近单位根序列和白噪声序列的检验表明，秩检验在T较小时（≤50）的功效很差，劣于传统单位根检验，RDF检验优于其余两种秩检验；在大样本情形，秩检验与传统单位根检验则相近。

（2）对于随机干扰项分布为有偏和厚尾情形，RDF检验不适用于取值恒为正的分布序列，其余两种秩检验的检验功效和检验水平都是不错的，其中逆正态得分秩λT(INS)要优于得分秩λT(uni)。

（3）当序列中有异常值时，秩检验较传统单位根检验稳健。对于单点异常值（AO），秩检验统计量的检验水平稍优于传统检验统计量，然而其对于近单位根的检验功效要远远低于传统DF检验；对于创新离群值（IO），秩检验的效果则较差，这些问题随样本量的增大而显著改善。

（4）对于序列相关的情形，当样本较小时，秩检验不如传统的DF检验和SP检验，而当样本充分大时，秩检验基本不逊于传统检验统计量。

（5）当序列中存在非线性单调变换函数形式时，传统检验统计量的检验水平受单调变换函数形式的影响非常明显，并且随样本量的增大进一步恶化；秩检验则有理想的检验水平，且受样本量的影响不大。故而对于时间序列中的非线性变换检测，秩检验具有明显的优势。