非参数方法及应用研究：混沌与分形特征分析

1.计算两股指的滞后期

应用自相关法、非线性相关函数法以及复自相关法计算两股指的滞后期，结果如表4-3所示：

表4-3　两股指序列各方法下的滞后期

由表4-3可知，应用不同的方法得到的滞后期是不一致的，这从侧面也反映了序列可能存在非线性性。

2.计算两股指的关联维数

利用G-P法，考虑Brock与Baek（1991）的建议，嵌入维m的取值从3到14，得到其分析图4-6：

图4-6　上证综指SZ（上）与深圳成指SC（下）的lnCm(ε)-lnε分析图

由图4-6可知，上证综指在-1.8与-1.6间曲线为直线，并在嵌入维等于6之后渐近稳定，计算其斜率，得关联维数大约为2.5757；而对于深圳成指则在-1.8与-1.4间曲线为直线，其在嵌入维等于5之后渐近稳定，计算其斜率，得关联维数大约为1.8952。

3.计算两股指的Hurst指数及周期讨论

利用R/S方法求沪深两市股指SZ与SC的Hurst指数分别为：0.98909929和0.99184079，可见均在1附近，说明两序列均为长记忆的，进一步分析两股指的周期性，结果如图4-7所示：

图4-7　上排（下排）从左至右分别为上证综指SZ（深圳成指SC）的R/S分析图及V统计分析图(www.xing528.com)

由图4-7可知，上证综指SZ的周期大约为900个交易日，深圳成指SC的周期大约为后1100个交易日。

4.计算两股指的最大Lyapunov指数及其i－y(i)图

利用小数据量法求两股指的最大Lyapunov指数，可得沪深两市股指SZ与SC的最大Lyapunov指数分别为：0.000174与0.000142，其i－y(i)图如图4-8所示：

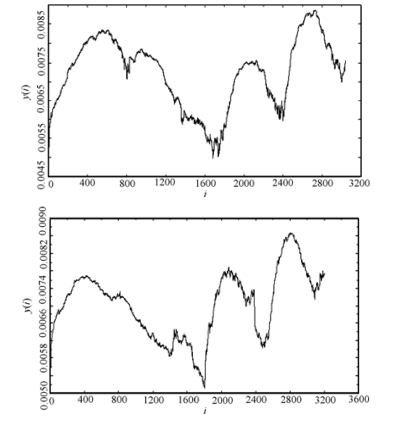
图4-8　从上至下分别为上证综指SZ与深圳成指SC的i－y(i)图

由图4-8可知，虽然两序列的最大Lyapunov指数均大于0，表明序列可能是混沌的，但轨线的第i个离散步后的距离对数ln(d(i))的平均值y(i)并未随离散步i的增加而趋于稳定，从而不能确定其存在混沌吸引子，两股指更可能是非线性非平稳的。

5.主要结论

本章对上证综合指数SZ与深圳成份指数SC序列是否存在混沌的最大Lyapunov指数值表明其为正，而i－y(i)图则不支持其有混沌吸引子，因此可认为两股指更可能是非线性非平稳的。应用Hurst指数对两股指序列的研究则表明其都是长记忆的，并表现出周期性。

【注释】

[1]关联函数的计算从文献看，主要有两种：一种是分母为M2，另一种为M(M－1)/2。本书认为，由于所考察的对象为相空间不相交两点，实际应用时选第二种较为合适。

[2]注意到计算中自相关函数的分母不变，与初始值相除会约掉分母，同时，物理学应用研究中一般为0，故而一般混沌研究文献中将自相关函数式取为。

[3]格里波基（1983）证明，只要最大的Lyapunov指数大于零，就可以肯定混沌的存在。故而对于时间序列是否混沌，只需看最大Lyapunov指数是否大于零。

[4]Parzen窗：。