非线性协整时间序列的非参数方法模拟结果分析

4.4.2.1　各模型的最大Lyapunov指数值的MC仿真结果

1.数值结果分析

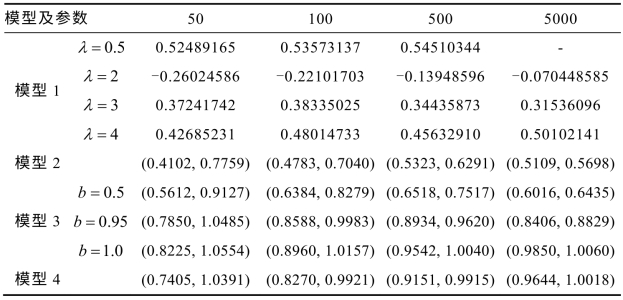
表4-1　小数据量法下各模型序列的最大Lyapunov指数

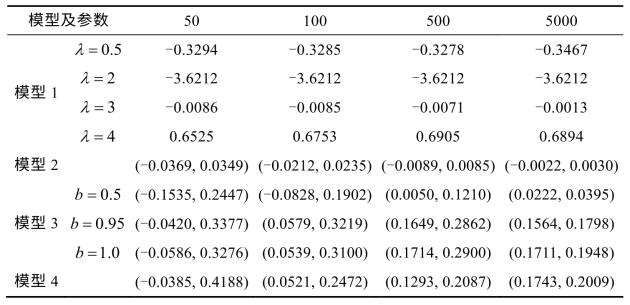
注：对于各随机序列，表中所给区间为按样本容量50，100，500，5000分别重复1000，1000，500，100次模拟得到的计算数值取5%～95%间的数值。

由表4-1可知，对于确定性模型1的各种情形，特别当λ＝4时，相对于其最大Lyapunov指数准确值0.693，本书对各样本容量的计算值误差不超过6%，能够准确反映序列是混沌或是空间收敛的；而对于高斯白噪声序列，按小数据量法计算的最大Lyapunov指数并没有确定的数值，其在0附近变化，并且随样本容量的增大，波动明显减小（详见后面的图形结果分析）；对于模型3，b = 0.5时为平稳序列，其最大Lyapunov指数值变动与高斯白噪声序列相似，但在0附近波幅更大一些，而当b = 0.95和b = 1.0时，其最大Lyapunov指数值变动明显右移，对于大样本容量不再出现负值，近单位根与单位根的区别在小样本并不明显，而当样本容量N为500和5000时，其区别见后面的i－y(i)图形分析。当序列为一个单位根或者模型4的情形时，其最初的表现与混沌序列是一致的，即在相空间轨线存在明显的分岔，数值计算则是最大Lyapunov指数为正，故而从最大Lyapunov指数数值为正并不能区别混沌与非平稳。但是，本书研究发现，利用i－y(i)图可以直观上分辩大样本下确定性混沌序列和随机非平稳序列间的区别。

2.图形结果分析

对于高斯白噪声序列，以样本容量分别为50和100为例，重复1000次的最大Lyapunov指数值变化频数图如图4-1所示：

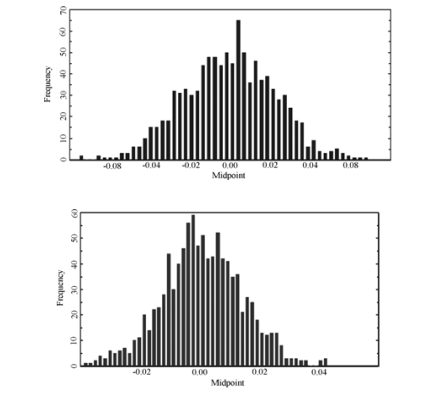
图4-1　样本容量分别为50和100的高斯白噪声序列的最大Lyapunov指数值变化频数图

由图4-1发现，对于高斯白噪声序列（事实上对于所有独立同分布序列都是如此），最大Lyapunov指数值会在0附近波动，并且还发现，随样本容量的增大会向0点集中。

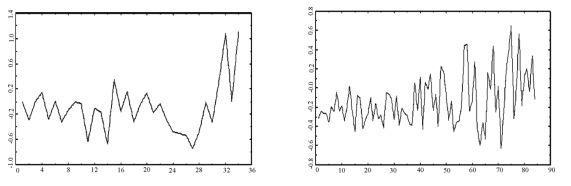
进一步考查计算Lyapunov指数的i－y(i)图，本书首先给出确定性Logistic映射序列的i－y(i)图4-2如下：

由图4-2发现，当λ小于4时，确定性Logistic映射序列是不同类型收敛的，曲线呈向右下方倾斜；而当λ等于4时，序列是混沌的，最初的变化是斜率为正，Lyapunov指数的几何意义是度量轨迹收敛或发散的比率，可以发现，最初两轨线间的分岔是迅速增大的，但当离散步到一定值时这样的发散则不再变化（注：曲线尾端的剧烈波动是算法的原因，与本身变化无关），也即呈现出吸引子的特征。为比较分析，可与图4-3所示的高斯白噪声序列的Lyapunov指数i－y(i)图相对照：

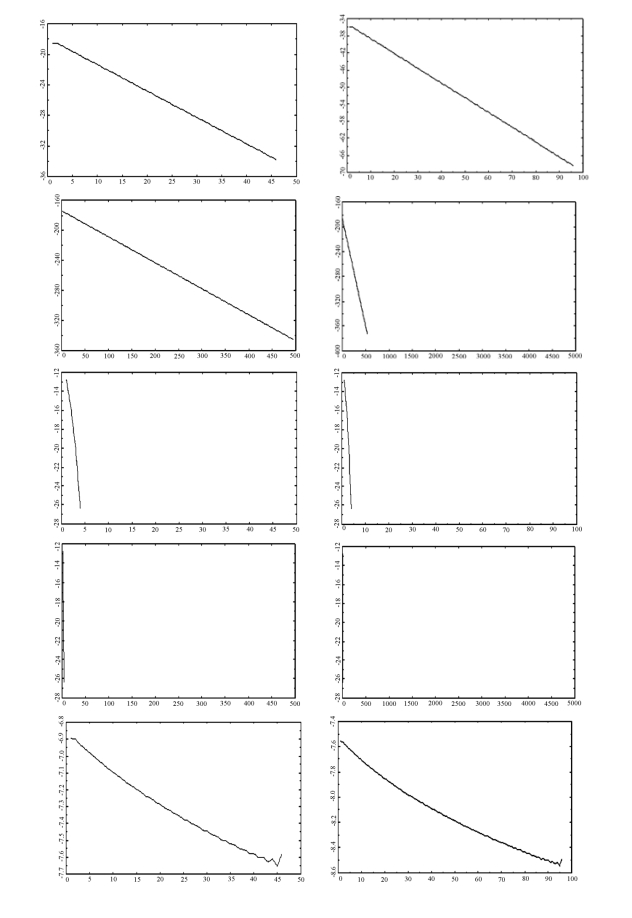
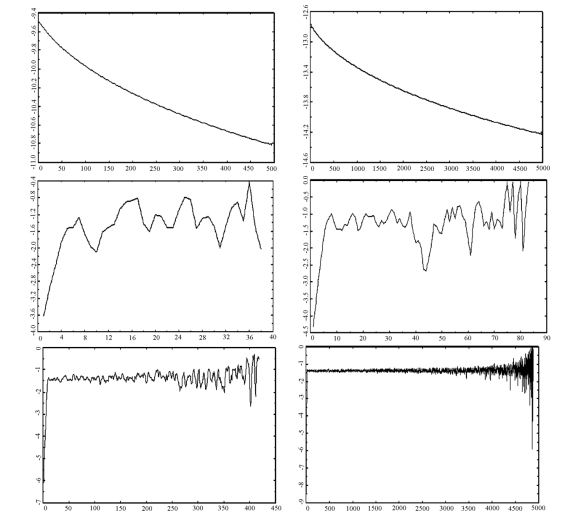
图4-2　确定性Logistic映射序列在λ＝0.5,2,3,4下从左至右容量分别为50，100，200，500，5000的i－y(i)图

由图4-3发现，对于小样本，还不能看出明显区别，但对于大样本，图中曲线不再有明显变化，呈现水平直线形式，也即最大Lyapunov指数应为0。

(www.xing528.com)

图4-3　白噪声序列从左至右容量分别为50，100，200，500，5000的i－y(i)图

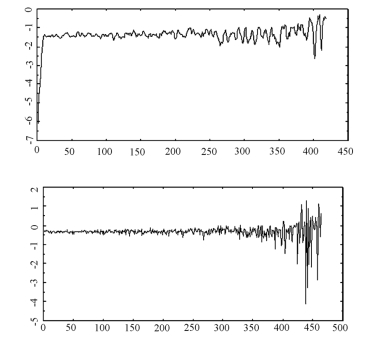
图4-4　样本容量为500时确定性Logistic映射序列（上）与白噪声序列（下）的i－y(i)图

由图4-4可以清楚地看到，存在吸引子的y(i)曲线最初是正斜率的增长，而高斯白噪声序列并不存在两轨线间的明显分岔，即在相空间中轨线变化不随离散步i的变化而变化。因此，从几何角度看，任何独立同分布的时间序列，其相空间的轨线分岔率都为0。

其次，本书发现，对于模型3，b = 0.5时为平稳序列，其最大Lyapunov指数的i－y(i)图与高斯白噪声序列相近；而对于近单位根的情形，如当b = 0.95时，小样本时和b = 1.0即单位根序列相似，但对于大样本，则有明显区别。考查N＝5000的情形如图4-5所示：

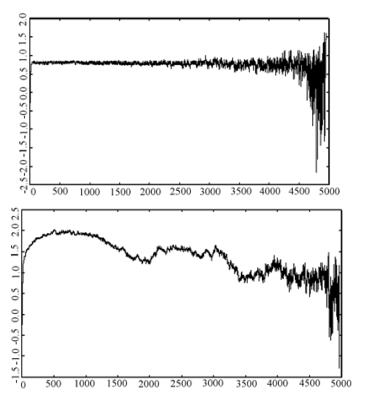
图4-5　样本容量为5000时近单位根序列（上）与单位根序列（下）的i－y(i)图

由图4-5发现，虽然近单位根序列的y(i)曲线最初是正斜率的增长，但随着离散步i的增加，y(i)不再有明显变化，表现为短记忆的；而单位根序列的y(i)仍然剧烈变动，表现为长记忆的。对于模型4，单位根序列的非线性瞬时变换序列，其i－y(i)图中y(i)曲线与单位根序列一样是剧烈变动的，表现为长记忆。

由此，可以得到一个结论，对于随机序列，应用小数据量法实现的最大Lyapunov指数值的意义在随机条件下和确定性混沌条件下是不一致的，Markellos（1997）提出的用最大Lyapunov指数为0来测度I(1)序列，用Lyapunov指数为负来测度I(0)序列，本书认为，在随机场合有待进一步商榷。而利用小数据量法计算最大Lyapunov指数得到的i－y(i)图，则可以直观地反映随机时间序列的记忆性。

4.4.2.2　各模型的Hurst指数值的MC仿真结果

由表4-2可知，利用R/S方法求Hurst指数会存在一定的误差，而且对于小样本，几乎难以准确地反映序列的真实Hurst指数，但从表中数值仍可清楚地反映出不同序列的Hurst指数的变化。当λ小于4时，确定性Logistic映射序列是不同类型收敛的，Hurst指数对λ为0.5时数值有问题，这是由于序列迅速收敛到0造成的计算问题；当λ等于4时，白混沌与随机白噪声表现相近，故数值在0.5左右。对于高斯白噪声，其小样本Hurst指数值波动较大，渐向0.5收敛；而对于模型3，Hurst指数值随b的增加而增大，并最终达到1左右，这从分形本身的几何意义可以解释，分形维反映了序列的自相似程度，显然Hurst指数值会随b的增大而自相似程度增加。模型4则是对随机游走过程取单调瞬时变换，这会降低序列的自相似性，因而Hurst指数值表现出稍低于b = 1的情形。

表4-2　R/S分析法下各模型序列的Hurst指数

注：对于各随机序列，表中所给区间为按样本容量50，100，500，5000分别重复1000，1000，500，100次模拟得到的计算数值取5%～95%间的数值。

由此，本书MC仿真研究发现，Hurst指数值在随机场合在1附近时大致可以反映序列的记忆性，但要求序列的长度不能太小，并且认为hurst﹥0.5就判断序列为长记忆的显然有待进一步商榷。