非线性协整时间序列分析-Hurst指数与R/S检验

R/S检验法首先由Hurst（1951）提出，其后，Wallis 与Mandelbrot（1968，1969）以及Mandelbrot（1975）发展了该方法。R/S检验法最初用以研究分形特征，也可用以求解Hurst指数，其后则被用于检验时间序列的混合性或长记忆性。

1.R/S检验统计量

R/S检验统计量的基本计算步骤如下：

设时间序列{xt,t＝1,2,…,N}，定义：

样本均值为：

样本方差为：

累积离差为：

极差为：

则R/S统计量的估计值为：

当存在短记忆和异方差的情形时，R/S统计量不具有稳健性，Lo（1991）提出修正的R/S统计量为：

其中

；

。

谱窗的选择也可以考虑Parzen窗（1962）^[4]，对于q值的选取，Andrews（1991）给出如下公式：

其中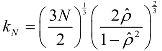；为一阶自相关系数。

Lo（1991）证明，在强混合条件下，统计量：(www.xing528.com)

V的分布函数为：

利用上式可以获得任意水平上检验的临界值，从而通过检验Vn的显著性来确定时间序列的混合性。

对于修正的统计量，则有

2.利用R/S统计量求Hurst指数

对于时间序列{xt,t＝1,2,…,N}，取其中n个序列的观察值，则序列被划分为m＝[N/n]个独立的长度为n的时间序列，计算各序列的R/S统计量，i＝1,2,…,m，进一步求该m个R/S统计量的平均值，可得长度为n的时间序列的R/S统计量的估计量：

对于不同的n值，可得R/S统计量序列，Mandelbrot（1979）证明：

其中C为常数，H为Hurst指数。即有：

两边取对数，可得：

由此，作出与logn的关系图，其斜率为Hurst指数H。

3.利用R/S检验统计量确定循环周期

方法一：通过绘制log(Qn)关于logn的图形来粗略估计。对于该图，每一个循环的结尾也就是下一个循环的开始，通过图中的转折点的位置，可以估计平均的循环长度。

方法二：利用Vn统计量。当n充分大时，Vn满足：

这里H为Hurst指数。

很显然，若H＝0.5，则R/S统计量是以时间的平方根标度的，过程是独立的、随机的，针对logn绘制的Vn统计量图应该是平坦的；若H﹤0.5，过程是反持久性的，图形应该是向下倾斜的；若H﹥0.5，则过程是持久性的，图形应该是向上倾斜的。当Vn图形的形状发生改变时，就产生了突变，长期记忆过程消失。通过Vn统计图，可以发现断点，检查在每一区间的Vn的最大值，从而估计每一频率的循环长度。方法二较方法一更精确。