相空间重构技术在非线性协整时间序列中的应用

利用实际中的时间序列来考察非线性系统中奇异吸引子的方法目前得到广泛应用的是Packad等人（1980）提出的延迟坐标状态空间重构法。

非线性复杂系统中包含多个变量，但通常情况下只能观测到其中某一分量的离散样本序列。设时间序列{xt,t＝1,2,…,N}为观测序列，Takens定理（1981）认为，根据一个变量的时间序列可以重构系统相空间。因为时间序列本身蕴涵了参与此动力系统的全部变量的有关信息，通过考察观测到的变量分量，将它在某些固定的时间延迟点上的观测量看成新的坐标，以张成一个多维状态空间，即重构的相空间。相空间的维数称为嵌入维数m，固定的时间延迟τ称为嵌入延迟，则相空间的点为：

其中t＝1,2,…,M,M＝N－(m－1)τ。

在重构空间中，嵌入维m与时间延迟τ的选取十分重要，其精度直接关系到相空间重构后描述奇异吸引子特征的不变量的准确度。关于τ和m的选取，目前主要有两种观点：一种是，Takens（1981）认为两者是互不相关的，即τ和m的选取可以独立进行（Takens证明了对于无限长的、无噪声干扰的时间序列，其τ和m是相互独立的）。另一种是，Kugiumtzis（1996）、Kim（1999）认为τ和m是相互关联的，因为现实中的时间序列都是有限长且不可避免地受到各种噪声的影响。本书主要采用第一种观点，分别求解现实时间序列相空间重构的嵌入维m与时间延迟τ。

1.嵌入维数的确定

选取m的方法通常为Grassberger与Procaccia（1983）提出的饱和关联维数的G-P法。

设相空间中不相交的两点为：

对于某一给定的临界距离ε，称相空间Rm中奇异吸引子上的两点间距离小于ε的概率为关联函数^[1]，记作：

其中Θ(∙)为Heaviside函数，即当u≥0时，θ(u)＝1，否则为构造相空间中两个相点之间的欧氏距离（亦可考虑其他范数形式）。

对于一个充分大的M(M→∞)，适当调整ε的取值范围，使得在一段ε的取值区间内有，此时，称为关联维数（或奇异吸引子维数）。

如果时间序列{xt,t＝1,2,…,N}有奇异吸引子存在，则Dm随着m的增加而增加，当Dm增加到一定程度时，Dm趋于饱和值D。对于混沌系统，D一般为分数。其几何意义也即画出lnCm(ε)与lnε图，求出其渐近稳定斜率。

G-P法的主要思想就是：选择不同的ε，分别计算相应的Cm(ε)，将这些不同的ε和Cm(ε)拟合出Dm。增加m，求出Dm的饱和值D。反过来，即可根据D确定合适的系统嵌入维数m。通常情况下，选取嵌入维数m≥2D＋1（Takens（1981）证明，如果延迟坐标的维数m≥2D＋1，在这个嵌入维空间里可以把有规律的轨线即奇异吸引子恢复出来，亦即在重构的Rm空间中的轨线上与原动力系统保持微分同胚，从而可以进行混沌时间序列的分析与预测）。

上述关于关联维数D的估计，需要恰当地选择ε的值，包括随后的一些估计方法，例如：Denker与Keller（1986）、Scheinkman与Lebanon（1989）使用OLS方法估计D，Cutler（1991）利用广义OLS方法估计D，Ramsey与Yuan（1989）利用随机系数回归等回归方法；另外，Brock与Baek（1991）使用了点估计，Smith（1992）提出了二项式估计等自由回归方法。这些方法对于ε的取值处理都是任意的和主观的，显然都会在一定程度上影响估计的精确性。Brock与Baek（1991）注意到这一点，他们提出：对于低维的非线性动力系统，嵌入维m的取值可在2与5之间，ε的取值可在与2σ之间，这里σ为原时间序列的标准差。Liu、Granger和Heller（1992）则继续沿用了Smith的方法，取εj＝φj，其中0﹤φ﹤1，j≥1，当j充分大时，可估计D。

2.嵌入延迟τ的确定(www.xing528.com)

在相空间重构时，需要确定时间延迟τ。对于实际的观测序列，因为存在噪声干扰和估计误差，如果τ太小，相空间轨迹会向同一位置挤压，信息不容易显露，从而产生冗余误差；如果τ太大，则会导致某一时刻的动力学性态与后一时刻的动力学性态发生剧烈的变化，使得简单的对象表现得复杂，动力系统信号失真，产生不相关误差。按独立求解的思路，目前主要有：（1）序列相关法，如：自相关法（Albano，et al.1988）、互信息量法（Fraser，1989）和高阶相关法（Albano，1991）等；（2）相空间扩展法，如：充填因子法（Buzug，1992）、摆动量法（Buzug，1992）、平均位移法（Rosenstein，et al.1994）和SVF法（Singular Value Fraction，SVF.Kember，Fowler，1993）等。

选择合适的τ，自然要求线性独立，自相关函数法是非常成熟的求时间延迟τ的方法。其思路如下：

对于时间序列{x(t),t＝1,2,…,N}，序列时间跨度为kτ的自相关函数^[2]为：

固定k，作出自相关函数关于时间τ（取τ＝1,2,…）的函数图像，当自相关函数Rxx(kτ)下降到初始值的时，所对应的时间t就是重构空间的最佳时间延迟τ。

关于非线性时间序列，由于自相关函数法只利用了序列间的线性相关信息，因此有必要进一步考察非线性相关的信息。本书介绍两种方法：

（1）Luis（1995）提出的非线性相关函数法。引入非线性相关函数，结合线性相关函数，使延迟时间τ的计算变为两部分：

式（4-15）检测序列的线性相关性，式（4-16）则检测序列的非线性相关性。设τx与τx2分别对应Φxx(τ)与的第一个极小值，则取

由于可以检测到Φxx(τ)检测不到的非线性相关性，因而该法会得到比自相关函数法求得的延迟时间要短。

（2）林嘉宇等（1999）提出的复自相关法。复自相关法是由自相关法和平均位移法结合推导出来的。其基本思路如下：

对于时间序列{xt,t＝1,2,…,N}，在m维相空间的平均位移可写为：

将式（4-17）展开并忽略边缘点带来的误差，有：

式（4-18）中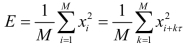：在1≤k≤m－1内为常数，Rxx(kτ)为序列的自相关函数。

令，则序列在m维相空间的复自相关法可描述为：当嵌入维m为某一确定值时，选取下降到其初始值的时对应的时间延迟τ。