混沌特征描述研究成果

描述混沌系统的重要特性指标包括：最大Lyapunov指数、Kolmogorov熵、关联维数等。

1.最大Lyapunov指数

由于混沌系统在初始状态的微小不确定性情况下将会迅速地按指数速度扩大，因此，在非混沌系统中，相互靠近的轨迹要么呈指数速度迅速收敛，要么慢于指数速度发散。混沌系统的这种轨迹收敛或发散的比率，称为Lyapunov指数，也即Lyapunov指数测度一个奇异吸引子中的两轨线间的分岔率。正的Lyapunov指数意味着混沌，而且它的维数是分数维。

最大Lyapunov指数表征系统的混沌性，同时表明系统的邻近轨线的辐散或辐合程度。混沌系统的最大Lyapunov指数为正数，随着时间的延长，邻近轨线的离散与否，意味着对初始信息的忘记或保留，即关系到可预报性问题，所以系统的最大可预报时间尺度可利用最大Lyapunov指数的倒数进行估计。

定义4-3　设X(t)是动力学方程＝F(X)的解，W(t)是切空间运动方程

的解，这里，则上极限

称为轨线X(t)的最大Lyapunov指数。

最大Lyapunov指数也可以利用Lyapunov谱来求得。Lyapunov谱是所有Lyapunov指数的集合。

定义4-4　对于一个n维系统的向量表达式：

其Jacobian矩阵为：

对该矩阵进行T次迭代后得到的矩阵记为JT，将矩阵JT的特征根按大小顺序

进行排列，记为：

则Lyapunov指数就定义为：

这里μ1为最大Lyapunov指数。

2.Kolmogorov熵

熵是动力学中描述系统无序程度的量，其概念源于19世纪40年代发展起来的信息理论，主要贡献者是Shannon、Renyi、Kolmogorov。Shannon最早将熵的概念引入信息论，提出信息熵（Shannon熵）的概念，用以刻画对系统无知的程度。

当不能得到轨线的精确初始值时，随着轨线的演化，解的发散意味着信息的丢失。在混沌系统中，Kolmogorov（1958）引进测度熵的概念，简记为K熵，用以度量系统的混沌程度。K熵反映信息损失的平均速率，代表了系统信息产生的频率。K熵定义如下：

定义4-5　对于动力学方程，其相空间具有有限体积（测度），给定相空间的一个有限分割α，每隔单位时间取样，即得一个符号动力系统。令N(n)是字长为n的允许字数目，对于每一个字长为n的允许字，存在着一个概率p，它正比于该允许字所具有的相体积。设pi，i＝1,2,…,N(n)，为第i个字长为n的允许字出现的概率，满足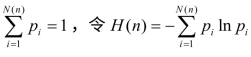，则系统的测度熵为：(www.xing528.com)

Kolmogorov熵也可以用Renyi熵来定义：记作一个划分，并将时间轴划分成时长为τ的小段。为系统中的一条轨

定义4-6对于一个动力系统，将其相空间分为各个边长为ε的小盒子，线，设p(i1,i2,…,in)为在第ik个盒子（k = 1,2,…,n）中的联合概率，则q阶Renyi熵定义为：

当q→1时，可得Kolmogorov熵K：

显然，K度量系统在单位时长内信息的平均损失的大小。由式（4-8）可以看出，K不依赖于ε。当系统的微分方程未知时，K难以计算，但事实上，Kolmogorov熵K是q阶广义熵（Renyi熵）的一个特殊情形。因为且为所有正的Lyapunov指数之和，并且Kq≥Kq＋1，只要K2﹥0，则必有K1﹥0，从而系统就是混沌的。一般情形下，K1与K2非常接近，K2是K1的一个好的估计，故而一般用K2熵作为Kolmogorov熵的近似。

K熵提供了动力学系统的重要信息：当K＝0时，系统表现为周期性规则运动，不产生新的信息；当K→∞时，系统是随机的；K为正常数时，系统则是混沌的。

3.关联维数

关联维数即奇异吸引子维数，用以定量描述奇异吸引子自相似的分形结构特征。对于奇异吸引子的维数的测度，Halsty（1986）提出了分数维测度（Fractal Measures）的概念，主要有盒维数（Hausdoff维数）、信息维数和关联维数。

定义4-7　对于由点集组成的d维空间中的一个奇异吸引子，以d维的小格子εd覆盖整个吸引子，设所需格子数为M(ε)，第k个格子中有Nk个点，pk＝Nk/N，则定义盒维数（Hausdoff维数）为：

盒维数存在两个问题：一是当奇异吸引子的维数较高时，其计算量巨大；其二是没有反映几何对象的不均匀性，各格子的权重相同。信息维数改进了第二个问题。

定义4-8　信息维数的定义为：

这里。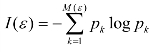

显然，盒维数是信息维数当各格子的权数相同时的一个特例。同样，信息维数也存在巨量的计算问题，因此，实际中广泛使用的是简单易算的关联维数。

定义4-9　关联维数的定义为：

这里C(ε)为关联积分：

其中。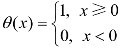

一般而言，对于规则图形，三个维数的值是相同的并等于图形所在空间的维数。但是，对于奇异吸引子，三个维数则不相同，并且是分数形式。