双谱检验方法及应用研究结果

Hinich（1982）以及Ashley、Patterson与Hinich（1986）提出了一个基于双谱分析方法（Bispectral Analysis）的非线性性检验。双谱分析是基于三阶矩的，其建立在如下结果之上：线性时间序列合适的标准化双谱对所有频率都是恒定的，而且在正态条件下，这个恒定值为0。双谱图分析的思路如下：

设{xt}为一个零均值的平稳序列，则可表述为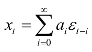：，其中{εt}是纯随机的，且权数{ai}是固定的。定义{xt}的二阶和三阶自协方差：

从而时间序列{xt}的功率谱和功率双谱为：

利用双谱图可以分析序列的非线性性：可以通过三维图画出双谱图，观察其图形，如果双谱图是平坦的，则数据是线性的；如果双谱图是不平坦的，那么数据则是非线性的。

对双谱做如下变换：

其中以及。

式（3-7）的平方根称为时间序列{xt}的偏度，其独立于频率(ω1,ω2)。对线性平稳序列，其值是恒定的；而当序列为线性高斯序列，则双谱对所有频率(ω1,ω2)恒为0。因此，可用该事实检验非线性。Hinich（1982）提出的检验统计量是基于频率对(ω1,ω2)的估计偏度的内四分位距（Interquartile Range），注意到对双谱统计量进行估计方法的不同，其分布和临界值可使用蒙特卡罗模拟给出。

Vance与Sawyer（1994）及张贤达（1996）给出了一种双谱估计的间接方法，本书借鉴这一方法同时计算功率谱S(ω)和双谱B(ω1,ω2)，并最后计算b(ω1,ω2)，具体步骤如下：

（1）将时间序列数据{xt,t＝1,2,…,N}分为m段，每段含有b个样本，在各个段中，各数据都减去该段的均值；(www.xing528.com)

（2）设{xl(i),l＝1,2,…,b}是第i段数据，估计各段的二阶累积量和三阶累积量：

其中s1＝max(0,－h),s2＝min(b－1,b－1－h)；

ss1＝max(0,－h,－k),ss2＝min(b－1,b－1－h,b－1－k)。

（3）分别取所有段的二段和三段累积量的平均值作为整个数据组的二阶和三阶累积量的估计：

（4）计算功率谱和双谱估计：

其中L﹤b－1。

（5）计算偏度估计：