基于系统检验法的Johansen协整检验法的应用成果

E-G两步法的一个明显不足是单方程估计存在有偏性。Johansen（1988，1991）提出一种系统估计方法，其基本思想是基于协整的ECM形式，利用完全信息极大似然估计法，将一个求极大似然函数的问题转化为一个正则约束条件下求最大特征根的问题，从而给出了协整向量的极大似然估计和协整检验方法：迹与最大特征根检验。

考虑n维I(1)向量yt的ECM形式为：

这里Γi,i＝0,1,…,p －1为n×n阶矩阵，εt～i.i.d(0,Ω)。

若向量yt存在k个协整关系（0﹤k﹤n），则由前述Granger表述定理，Γ0可分解为Γ0＝－BA′，A,B都为n×k阶矩阵，则讨论的目标是确定k并估计A,B。

首先，式（2-53）的对数似然函数为：

对上述对数似然函数最大化。为求Γ0，可先将Γ0看作一定，对其他参数求其极大似然估计，然后再对Γ0求极大似然估计。即固定Γ0，对其余参数求极大似然估计为：

从而对Γ0集中的似然函数为：

注意到与Δyt－i,i＝1,2,…,p －1正交，现分别以Δyt,yt－1对Δyt－i,i＝1,2,…,p －1做两个辅助回归，得到两残差R0t和R1t，则两残差都与Δyt－i,i＝1,2,…,p －1正交，从而R0t－Γ0R1t也与Δyt－i,i＝1,2,…,p－1正交。由正交投影的唯一性，有＝R0t－Γ0R1t，进而可证明：^[6]。因此可进一步将式（2-55）表述为：

其中K0＝－Tn/2ln(2π)－Tn/2。

进一步，令两辅助回归残差的二阶矩为：

，且将Γ0＝－BA′代入式（2-56），则有：

令∂L*(A,B)/∂B＝0，可得：

将式（2-58）代入式（2-57）得到对协整向量A集中的对数极大似然函数：

对式（2-59）求极大值即对其中求极小值。而

因为A非唯一确定，可对A施加约束A′S11A＝Ik，则对式（2-60）的极小值问题可转化为如下条件极值问题：

进一步又可转化为求（或）的特征根。设其特征根为λ1≥λ2≥…≥λn≥0，对应的特征向量矩阵为V＝(v1,v2,…,vn)，且满足V′S11V＝In^[7]，则前k个特征值λ1,λ2,…,λk对应的特征向量矩阵(v1,v2,…,vk)满足式（2-61），即协整向量A的极大似然估计为：

则。从而其余参数的极大似然估计为：

Johansen（1988）证明了分别为Γ0,Ω的一致估计，Gonzalo（1990）则证明了为A的超一致估计。(www.xing528.com)

其次，由上述讨论，可进一步给出协整关系的检验。

将估计量代入式（2-59）得：

对于原假设存在k个协整关系，即H0:λk﹥0,λk＋1＝λk＋2＝…＝λn＝0，受此约束的对数似然函数为式（2-62），而不受此约束的对数似然函数为：

从而构造似然比函数，即迹检验（Trace Test）统计量为：

Johansen（1988）推导了该统计量的渐近分布为：

这里w(∙)为n－k维标准布朗运动。实际应用时可进行MC模拟确定临界值。

注意到λk＋1＝0，则λk＋2＝…＝λn＝0，故而可构建H0:λk＋1＝0，H1:λk＋1﹥0，似然比统计量即λ－max统计量为：

目前，这两种检验都有成熟的软件实现。

Johansen方法和E-G两步法相比，适用于多个协整关系的估计和检验，具有相对较高的检验功效。但这两种检验方法可能会产生冲突，另外，E-G两步法更为稳健。另一个不足是Johansen方法对滞后长度敏感。再有就是，Johansen方法没有解决当存在多个协整关系时，哪一个用以刻画长期均衡的协整关系。

【注释】

[1]详情可参阅汉密尔顿（1999）的中译版。

[2]一般地，可用Newey与West（1987）提出的核估计量：其中，w(j)＝1－j(l＋1)－1为核权数，滞后截断l＝o(T1/4)，可通过AIC准则或BIC准则判定。

[3]二阶布朗桥v2(s)可表为：。

[4]一般地，可用Newey与West（1987）提出的核估计：其中w(j)＝1－j(l＋1)－1为核权数，滞后截断l＝o(T1/4)，可通过AIC准则或BIC准则判定。

[5]Granger（1974）仿真模拟表明，对两个不相关的随机游走序列进行OLS回归，发现其判定系数R2很高，表现出具有相关性，但其DW值较低，这一现象称为伪（Spurious）回归现象。Phillips（1986）、Endorf（1992）进一步对该现象的原因进行了探讨，国内学者王少平（2002）、李美洲（2008）也对其进行了研究分析。一般而言，伪回归是指非平稳序列之间并不存在长期均整关系而在数字上出现某种巧合即表现出拟合优度、显著性水平等指标较好的情形。

[6]

[7]若特征根λi,i＝1,2,…,n 的特征向量为wi,i＝1,2,…,n，这些特征向量彼此正交，设wi′S11wi＝ki,i＝1,2,…,n ,则满足正则化条件的特征向量为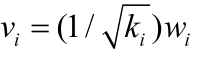注：由于S11为正定矩阵，因而ki﹥0）。