【摘要】：Schmidt与Phillips提出了一个得分统计量，此得分统计量用以检验差分平稳与趋势平稳，称之为SP检验。SP检验考虑的模型为：检验的原假设H0:序列{yt}为一带漂移的随机游走；备择假设H1:序列{yt}是趋势平稳的。Schmidt与Phillips构造的检验统计量为：对于无截距情形，有：则在原假设成立的条件下，当T→∞时，有：这里，为标准布朗桥。这里，调整后的SP检验统计量为：调整后的统计量与原检验统计量的分布相同。
Schmidt与Phillips（1992）提出了一个得分统计量，此得分统计量用以检验差分平稳与趋势平稳，称之为SP检验。
SP检验考虑的模型为：
检验的原假设H0:序列{yt}为一带漂移的随机游走；备择假设H1:序列{yt}是趋势平稳的。即原假设对应的模型为：
备择假设对应的模型为：
其中{εt}为i.i.d序列，均值为零，方差为σ2。
利用OLS对式（2-20）进行去趋势后，有：
令部分和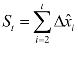
，则若原假设成立，即考察方程：
检查系数是否满足φ＝0，从而将其转换为DF检验的模型形式（2-3a）（2-3b）（这里讨论时常用第二种无截距情形，即式（2-23b））。
Schmidt与Phillips（1992）构造的检验统计量为：(www.xing528.com)
对于无截距情形，有：
则在原假设成立的条件下，当T→∞时，有：
这里
，
为标准布朗桥。
若考虑到可能的序列相关，则有：
其中，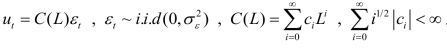
且C(1)≠0。
则应与PP检验分析相同：令
为εt的方差，记部分和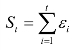
，则
，其一致估计
用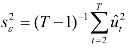
来代替；σ2≡λ为εt的长期方差，记部分和
，则
，其估计思路与PP检验一样可使用非参数核估计[4]。这里
，调整后的SP检验统计量为：
调整后的统计量与原检验统计量的分布相同。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
