关于非线性协整模型,已有多种研究形式,常用的有:双线性模型、非线性移动平均模型、非线性可加模型、门限协整模型等。如果非线性回归函数已知,则可用非线性最小二乘法估计模型的参数,并根据参数估计量的分布进行检验。但是,在实践中,变量之间的非线性关系的形式往往是未知的,因此,需要探讨利用非参数估计方法来实现对未知函数形式的估计。目前,主要有如下三种非参数估计方法。
(1)ACE算法研究。Granger和Hallman(1991)、Meese和Rose(1991)、Chinn(1991)开发了能得到基于定义1-1的变量的非线性变换的非参数交替条件期望(Alternating Conditional Expections,ACE)算法。ACE是一种非参数算法,只需要非常弱的分布假设,就可以处理数据的各种各样的非线性变换。Friedman(1985)证明,ACE算法给出的变换将渐近收敛于其最优变换。
(2)局部核权最小二乘法。局部核权最小二乘法是一种基于核函数的非参数检验方法。Nadaraya(1964)和Wat-son(1964)提出了非参数回归模型的核估计,其思想相当于将回归函数按局部零阶台劳展开的加权最小二乘估计。Stone(1977)和Cleve-land(1979)研究了回归函数局部线性台劳展开的核权最小二乘估计。Mach与Müller(1989)以及Chu与Mar-ron(1991)进一步研究表明:当解释变量是随机变量时,Nadaraya-Watson核估计的方差和局部线性回归估计相同,但偏多了一项。Fan(1992,1993)以及Fan与Gijbels(1992)发现,局部线性拟合不必进行边界修正,它在边界的偏差会自动与内部的偏差有相同的阶,因而局部核权线性回归估计较N-W核估计有更好的性质。Ruppert和Wand(1994)将一元局部线性回归估计结果推广到了多元情形。
(3)基于神经网络的非参数估计方法。基于神经网络的估计方法也是一种不需要选择模型的非线性形式的方法。由于应用非参数方法进行核函数估计可能会有维数灾祸问题,故应用神经网络来逼近未知函数则不失为一种较好的选择。20世纪80年代神经网络迅速发展,较为代表性的文献有Cybenko(1989)、White(1988,1989)、Hornik et al.(1989)、Kuan and White(1990)、
Barron(1991)以及Kuan and Liu(1995)发表的论文。神经网络可以无限逼近未知的非线性结构,因此,其在非线性协整理论的估计研究中具有重要的应用前景。(https://www.xing528.com)
根据以上分析,本书的技术路线如图1-1所示:
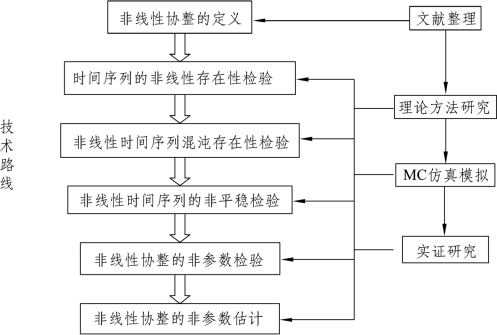
图1-1 本书技术路线结构框架图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




