任何关于强度和安全性问题的理性解决方法都隐含着这样的假设:工程师应该能够准确地预测一个计划建造的新结构的强度,即便他自身也会怀疑它预计能用多久。对诸如绳索、链条、直梁与支柱之类的简单结构,情况可能大致如此;但是,正如我们在第4章中看到的,对更精密和更重要的人工制品来说,比如飞机和船舶,情况则完全不同。
因为有关于各种不同结构的大量经验可用,有针对这一课题的大量高质量的数学文献,还有学院派的弹性研究者引以为傲的关于结构理论的长篇大论的演讲,所以这种疑虑可能会被视为庸人自扰。然而,它是对的。
例如,考虑一下关于飞机强度的统计数据。因为节省重量很重要,也因为失效的后果非常恐怖,所以飞机的结构设计自然要倾注许多细致的考虑与思考,每个细节都要一丝不苟地检查。制图和计算是由技艺精湛的设计师、应力分析师和制图员运用最科学的方法完成的。之后,强度的计算会交给一组完全不同的专家进行独立核验。因此,最终做出的强度预测要尽可能准确和缜密。最后,为确保万无一失,还要进行全尺寸机身的破坏实测。
要给出真正的最新结果是不可能的,因为近年极少有不同类型的飞机被订购,以致这些数据并不具有统计学上的显著性。然而,随着飞机变得更简单也更便宜,相当多的设计至少走到了原型阶段。1935—1955年,英国制造出差不多100种不同的飞机并进行了破坏测试。因此,这一时期的结果具有相当可靠的统计学意义上的指导性。
当然,这些不同类型飞机要求的强度的实际数据千差万别,要根据飞机的大小和类型而定。但是,每个设计团队的目标都是,让强度达到行话所谓的“120%全因子载荷”。[3]如果结构设计完全是一个严谨的专业,当绘制曲线或“直方图”时,人们就可以预期,各种测试结果紧密聚集在120%全因子载荷值的附近,偏差极小。换言之,结果应该产生一条狭窄的“正态”或钟形曲线,如图15-1所示。
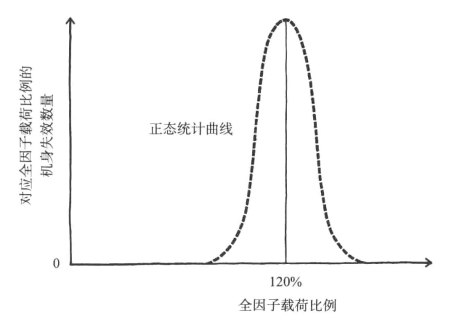
图15-1 实验飞机强度的预期统计分布(https://www.xing528.com)
众所周知,这类事情压根儿没有发生。当把结果绘制成统计图时,直方图看起来很像图15-2。实验强度倾向于随机分布在约50%~150%的要求载荷或全因子载荷之间。也就是说,即使是最卓越的设计师,也不能指望他在上限是下限三倍的区间内准确预测飞机的强度。其中一些飞机的强度还不到应有的一半;而另一些的强度又太大,以至于比所需重量沉得多。
对船舶来说,实在找不到数据来支持这种判断——因为几乎从未有船舶在实验室条件下做过破坏测试。所以,我们不可能知道船舶工程师的工作做得多好或多糟,至少在强度预测方面是这样。然而,我们在第5章中说过,船舶的结构性事故的数量相当可观,时至今日,每吨英里的事故数量似乎很有可能仍在增加。
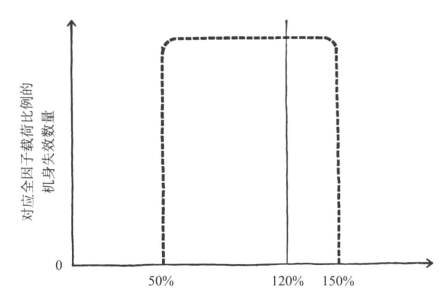
图15-2 1935—1955年,测试架上被破坏机身强度的实际分布(非常近似的示意图)
至于桥梁,其强度计算问题在某些方面要比船舶和飞机容易,因为其负载条件的变化较少。尽管如此,现代桥梁的失效数量还是十分巨大的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




