20世纪可能会被后世称为“钢材与混凝土的时代”，它也可能被称为“丑陋的时代”，或许还有其他不中听的名字，比如“浪费的时代”。不仅是痴迷钢材和混凝土（而对外观漠不关心）的工程师，政客与路人似乎也感染了同样的“病”。这种病可能源于200年前的工业革命与廉价的煤（又带来了廉价的铁），它使得铁制蒸汽机足以将煤转化为便宜的机械能：在能量越来越密集的循环里，往复不休。因此，煤炭和石油存储的大量能量被塞进小型体积中。发动机在很小的空间内非常迅速地处理了大量能量，然后它们会以电功或机械功的形式集中输出能量。我们所有的当代技术都依赖于这种能量的汇集。这项技术的材料——钢材、铝材和混凝土——本身就需要大量的能量来制造，表14-1显示了它们需要多少能量。因为需要这么多的能量来制造，这些材料就只能在能量密集型经济中使用并获利。我们不仅为技术设备投入货币资本，还得投入能量资本，两种投资都有必要确保合理的投资回报。
表14-1 生产不同材料所需能量的近似值
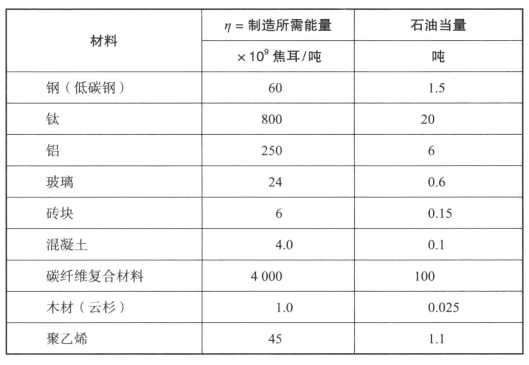
注：所有这些数值都非常粗略，无疑也是有争议的，但我认为它们都处于正确的区间。碳纤维复合材料的取值无疑是个估测值，但它是基于多年开发同类纤维的经验得到的。
尽管能量的成本很高且日益稀缺，但能量密集化的趋势只增不减。先进的发动机，比如燃气涡轮机，在越来越小的空间内越来越繁忙地处理越来越多的能量。先进的设备需要先进的材料，而更新颖的材料，比如高温合金与碳纤维塑料，在制造过程中又会消耗越来越多的能量。
想必这种方式的确不能持续太久，因为整个系统完全依赖于廉价而集中的能源，比如石油。生物界可被视为一个庞大的能量提炼系统（能量的来源不是集中的而是分散的），再以最经济的方式使用这些能量。目前，正在进行的许多尝试是从分散的来源收集技术所需的能量，比如太阳、风或者海洋。其中许多尝试很可能会失败，因为所需的能量投入——采用常规的钢制或混凝土制的收集结构——不能产生经济回报。我们需要用完全不同的方法来处理“效率”的整体概念。大自然似乎是根据它的“代谢投入”来看待这些难题的，我们可能也需要这样做。
不仅是每吨金属和混凝土都需要大量能量来制造（见表14-1），而且对低能量密集度系统通常所需的分散或轻负载结构而言，用钢材和混凝土制成的设备的实际重量，很可能比我们使用更合理和更文明的材料要高出许多倍。
我们很快会看到，从严格的结构学意义上说，木料是最“有效”的材料之一。对于大尺寸和轻载荷的情况，木制结构比钢制或混凝土制结构要轻得多。在过去，围绕木料的困难之——直是，树木生长要花很长时间，而木材价格的涨落会随季节变化。
最近几年，材料领域最重要的发展或许是植物遗传学家的功劳，他们培育出快速生长的商用木料品种。因此，如今种植的美国五叶松在顺利的情况下，其直径每年会增加12厘米，6年后便可长成适于砍伐的成熟木材。所以，木材具有优良的收获前景，它们可以在短时间周期内长成，而其生长所需的能量几乎都是由太阳慷慨赠予的。据推测，当有人用完一个木制结构时，可以通过燃烧方式释放其木料在生长过程中收集的大部分能量。当然，钢材或混凝土不行。
此外，木料过去常常需要在加热窑炉中进行漫长又昂贵的干燥处理，这也得消耗大量的能量。近期的研究结果表明，现在我们可以以非常低的成本在24小时内完成相当大的软木方材的干燥处理。这些都是关乎结构和世界能源形势的非常重要的发展，我们理应有所考虑。
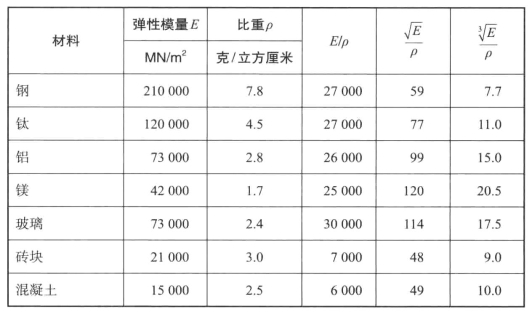
附录Ⅳ给出了关于不同作用结构的效率和不同材料的重量的一些代数分析。许多高技术含量结构的设计，比如飞机，主要受制于E/ρ准则，即“比模量”，它控制着总挠度的重量成本。碰巧的是，对于大多数传统结构的材料，比如钼、钢、钛、铝、镁和木材，E/ρ的值应是常数。正是出于这个原因，在过去的15或20年里，政府投入巨额资金来开发基于硼、碳和碳化硅之类的新奇纤维的新材料。
这类纤维在航空航天领域可能有效，也可能无效；但似乎可以确定的是，它们不仅很昂贵，还需要消耗大量的能量来制造。出于这个原因，它们未来的用途很可能相当有限，在我看来，它们在可预见的将来不太可能成为“大众材料”。
严格又昂贵地控制总挠度的要求，可能效果非常有限；然而，如我们所见，承载压缩载荷的重量成本——经常还有资金成本——往往非常高。立柱承载压缩载荷的重量成本不是受制于E/ρ，而是取决于
；板的重量成本则受制于
（附录Ⅳ）。表14-2汇总了这些要求。显然，低密度的情况有很高的溢价。因此，钢材的表现相当糟糕，甚至比不上砖块和混凝土。而且，对许多轻量级的应用，比如飞艇或假肢，木材甚至比碳纤维材料更好，而且更便宜。
表14-2 不同作用的各种材料的效率(www.xing528.com)
（续表）
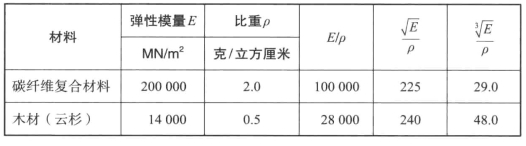
在表14-3中，这些长处体现在能量成本上。在这里，传统材料——木材、砖块和混凝土——的优势是压倒性的。这张表让人想弄明白，追求基于奇特纤维的材料是否真的合理。就大多数常见的生活用途而言，真正可获利的材料不是碳纤维，而是孔洞材料。很久以前，当大自然创造出木头时，它就领悟出这个道理了；当古罗马人开始用空葡萄酒瓶建造教堂时，亦同此理。不论是在资金上，还是在能量上，制造孔洞材料都比使用任意可能形式的高刚度材料更便宜。或许更好的做法是，把更多的时间和金钱花在开发蜂窝材料或多孔材料上，而少投入到硼或碳纤维上。
表14-3 不同材料（依据制造所需能量）的结构效率
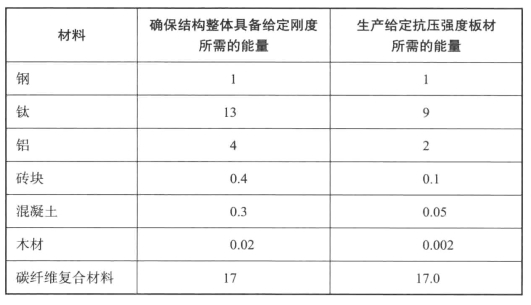
这些数据统一以低碳钢为单位基准，且仅为近似值。
【注释】
[1]可参考A.G.M.Michell，“The limits of economy of material in frame structures”，Phil.Mag.Series 6，8，589（1904）。
[2]因为承张杆的横截面积与载荷成正比，而终端配件的体积随载荷的3/2次幂增加。
[3]以代数方法来思考，我们可以将n个长为L的平行承张杆上承载载荷P的问题转化为如下形式：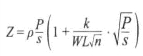
其中，Z=所有承张构件单位长度的总重量，P=总承载载荷，s=安全工作应力，k=与设计者才智相关的一个待定系数，W=材料的断裂功，n=承张构件的数量，ρ=材料密度。
这个式子的证明详见考克斯的《重量最小结构的设计》，我已对考克斯的公式略做修正。
[4]“阿波罗也无法一直拉开他的弓”（Horace，Odes II，x，19）。贺拉斯或许知道白银的蠕变几乎同铅一样严重。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
