到目前为止,我们所讨论的一切只适用于支杆和其他相当短粗的承压构件。我们看到,这些东西通常的承压失败是由于对角剪切机制,有时是因为纤维上形成的局部折痕。然而,大量不同承压结构含有的构件又长又细,并且以完全不同的方式失效。一根长杆或者一张薄膜,比如一个金属薄片或一页书,因屈曲而承压失败,这极易从最简单的实验中看出。(拿出一张纸,试着对其进行纵向压缩。)这种失效模式——具有重大的工艺和经济价值——被称为“欧拉屈曲”,因为它最初是由列昂哈德·欧拉分析产生的。
欧拉出身于一个以数学才能闻名于世的日耳曼裔瑞士家庭,他没用多久便获得了数学家的名望:在相当年轻的时候,他便应女沙皇伊丽莎白的邀请前往俄国。他一生的大部分时间都在圣彼得堡宫廷度过,当俄国政治局势动荡不安时,他应普鲁士的腓特烈大帝之邀一度避居波茨坦。18世纪中叶,在开明君主治下的宫廷生活一定既趣味十足又丰富多彩,但这一点极少反映在欧拉的鸿篇巨制中。据我所知,在所有关于欧拉的传记中,似乎极少有关于他的俗世趣味的记载。[5]他把所有时间都用来研习数学,并写成了海量的学术论文,这些论文在他辞世40年后还在发表。
事实上,欧拉其实根本无意于研究支柱。实际情况是,在他的诸多数学成就中,有一个叫作“变分法”,而他正欲找寻一个问题来小试牛刀。一位友人建议他可以用这个方法计算一根细竖杆在其自身重量作用下屈曲的高度。用变分法来解决这个纯假想的问题是很有必要的,因为,如我们在第3章提到的,应力和应变的概念直到很久以后才被发明出来。
用现代术语来表述,欧拉琢磨出来的东西就是我们今日所谓的“支杆屈曲载荷的欧拉公式”,即:
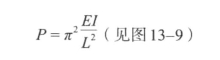
其中,P=柱或板屈曲处的载荷,E=材料的弹性模量,I=杆或板横截面积的二阶矩(即转动惯量,见第11章),L=支杆的长度。当然,所有这些量必须在同一单位制下。
(奇怪但又便利的是,这么多重要的结构公式在代数上竟如此简单。[6])
欧拉公式适用于各种各样细长的支柱和支杆(不论实心还是空心),或许更重要的是,它还适用于飞机、船舶,以及机动车上的薄板、薄盘和薄膜。
因此,如果我们为支杆或板绘制其破坏载荷对应其长度的图像,就会得到如图13-8所示的曲线,该图揭示了两种失效模式。对短支杆而言,失效是由压碎引起的。当长度与厚度之比增加到5~10时,这条线会与代表欧拉屈曲破坏的曲线相交。屈曲现在变成了更弱的模式,故而长支杆会以这种方式失效。在实践中,从压碎失效到欧拉屈曲的转变并不是一个突变,而是存在一个过渡区间,如图中虚线所示。
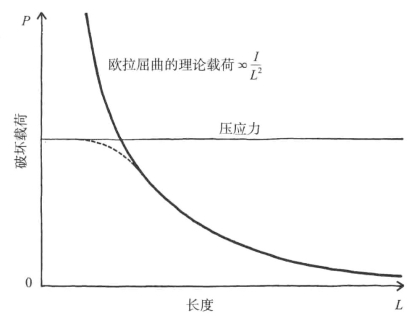
图13-8 支柱抗压强度随其长度的变化
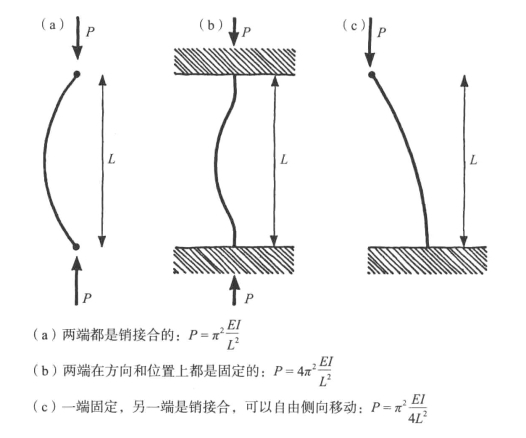
上文的欧拉公式假定杆或板的两端都是“销接合的”,或者是铰接合的(见图13-9)。通常,防止杆或板在末端铰接的任何东西都会增加屈曲载荷。对于两端都受到刚性约束的极端情况,屈曲载荷P差不多要乘以4。然而,要实现任何端部约束,往往涉及额外的重量、复杂性和成本,可能并不值得。而且,“刚性”的端部连接会将端部附件的任何偏差传递到支杆上。如果发生这种情况,支杆可能会提前弯曲,所以在实践中,它会变得更脆弱。因此,将桅杆“刚性”地连接到甲板和龙骨上,已不再是常见做法(见图13-10)。
 (https://www.xing528.com)
(https://www.xing528.com)
图13-9 各种情况下的欧拉公式
图13-10 如果支柱因两端被夹紧而被迫偏离直线,其屈曲载荷就会减小。因为索具易于拉伸,所以将桅杆固定到甲板和龙骨上已不再是通常的做法
注意,在我们刚才写下的欧拉公式中,没有代表断裂应力的一项。给定长度的杆或板上的屈曲载荷完全取决于横截面的“I”(或横截面积的二阶矩)及其材料的弹性模量或刚度。一根长的支杆在屈曲时不会“断裂”,它会以弹性弯曲的方式避开载荷作用。如果屈曲不曾超越材料的“弹性极限”,那么当载荷移除时,支杆会再次弹开伸直并恢复原状。这个特性通常是一件好事,因为可能据此设计出“牢不可破”的结构。宽泛地讲,这就是地毯和门垫的工作原理。不出所料,大自然非常广泛地运用了这一原理,尤其是对像青草这样的难免遭到踩踏的小型植物。这就是为何在草坪上行走而有可能不会造成任何损害的原因。正是由于荆棘尖刺与欧拉定理的巧妙组合,使得树枝篱笆对人和牲口来说几乎都是打不烂和穿不过的。同样,使用细长尖刺武器的蚊子和其他昆虫在叮咬你时也要靠结构上的技巧来避免这些细杆的屈曲。
在欧拉的一生中,其公式的实际技术用途非常少。在实践中,它唯一重要的应用就是设计船桅和其他圆杆。然而,同时代的造船者已经用务实的方法驯服了这个难题。了不起的18世纪造船教科书,比如斯蒂尔的《桅杆、船帆与帆索的制造基础》(Elements of Mastmaking,Sailmaking and Rigging),基于经验给出了各种尺寸桅木的通用表格,但这些推荐数据是否可以通过计算来加以改善就十分值得怀疑了。
在欧拉时代之后又过了大约一个世纪,人们才真正对屈曲现象产生了兴趣,这主要归功于锻铁板在建造施工中的应用日益增加。这些板材显然要比工程师惯用的砖石和木工结构薄得多。这个难题第一次得到认真对待是在1848年左右处理梅奈悬索桥期间。这座桥的设计工作是由三个杰出的人共同负责的,他们分别是:罗伯特·史蒂芬孙,数学家兼第一批工科教授之一的伊顿·霍奇金森(Eaton Hodgkinson),以及在结构中运用锻铁板的先驱威廉·费尔贝恩爵士(Sir William Fairbairn)。
史蒂芬孙的悬索桥最终失败了,因为它们的弹性太强了。英国海军部坚持桥下要留有100英尺(约30米)的净空高度以利通航,这也在情理之中。将必要的刚度和所需的净空结合起来的唯一办法,似乎是设计一座比现存桥梁都更长的梁式桥。出于种种原因,对每一个要求长度为460英尺(约140米)的梁,似乎最好用锻铁板组合制成管道的样式,让列车在管道内通行。
很快人们发现,最要紧的设计难题之一出现在铁板的屈曲上,这些铁板构成了梁的上部或承压面。虽然欧拉公式对于简单的板和杆足够精确,但桥管的形状无疑是复杂的,那时还没有适用的数学理论。因此,三位设计者别无选择,只好使用模型做实验。不出所料,这些模型被证明是含糊不清且不可靠的,三人因此发生争吵,合作关系一度近乎破裂。但是真正安全的管道设计仍没有什么头绪。最终定下来的是一种多孔箱式梁(见图13-11)。每个人都长出一口气,这种设计被证明是符合要求的,它一直撑到了1970年。
图13-11 布列坦尼亚桥:管状箱式梁
在史蒂芬孙的时代,人们对薄壳的屈曲进行了大量的数学研究,但这类结构的设计仍伴以大于通常程度的不确定性。所以,发展这类关键结构很可能花费昂贵,因为在设计落地前可能需要做全尺寸的强度测试。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




