结构尺寸与安全预测-结构是什么

虽然一些结构据说是靠信仰的力量来维持的，另一些则全靠涂料或铁锈结合在一起，但是，除非设计者毫无责任心，否则无论他打算建造什么，都倾向于获得关于其强度和稳定性的某种客观保证。如果不能做恰当的现代计算，那么显而易见，他应该做的事情要么是制作一个模型，要么是按比例放大某些之前已被证明可行的较小版本结构。

当然，这就是人们过去常做的事情，直到最近。或许他们现在仍然如此。问题在于，如果只是想看这东西长什么样子，那么这些模型都很好，但若要用它们来预测强度，则会有危险的误导性。这是因为，当我们按比例放大时，结构的重量会随尺寸的立方增大；也就是说，如果我们将尺寸增加一倍，重量就会增大到8倍。然而，必须负载结构重量的各部分横截面积只随尺寸的平方增大，也就是说，在两倍大小的结构中，这些部分的面积是原来的4倍。应力会随尺寸线性上升，若我们将尺寸增加一倍，应力也会增加一倍，这样一来，我们很快就会陷入严重的麻烦。

所以，任何可能因材料断裂而失效的结构，其强度不能根据模型或凭借先前的经验按比例扩大来预测。

这个原理是伽利略发现的，叫作“平方-立方律”，它可以很好地解释车辆、船舶、飞机和机械的设计，为什么需要依靠适当的现代分析方法。正因如此，这些事物直到近代才发明出来，至少是发展出它们的现代形式。但是，对大多数砖石建筑物而言，我们之所以能忽略平方-立方律，是因为就像我们说的那样，建筑物在正常情况下不会因材料受压破裂而坍塌。砖石建筑中的应力很低，以至于我们几乎可以无限地按比例将其放大。不像大部分结构，建筑物的坍塌是因其变得不稳定而倾覆；对任意大小的建筑物来说，这都能根据模型预测出来。

从哲学角度看待这个问题，建筑物的稳定性与天平或杆秤这类称重器的稳定性没什么区别（见图9-17）。两边的倾覆力矩都与其尺寸的四次幂成正比；如果我们按比例放大，一切都会保持平衡。因此，如果一座小型建筑物能站立不倒，那么按比例放大的建筑物也能屹立不倒；而且，中世纪建筑工匠的“秘诀”主要就是把这种经验转化为一系列的规则和比例。然而，我们能确认的是，他们也会使用由砖石或石膏制成的模型——有时长达60英尺（18米）。这种工序模式普遍适用，甚至是极其复杂的结构，比如兰斯大教堂（见图9-18）。

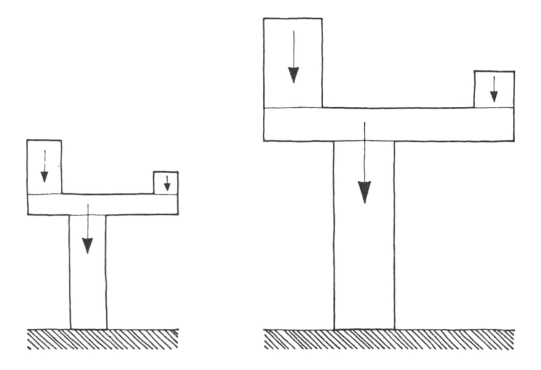
图9-17　建筑物的稳定性就像天平一样，不受比例放大的影响

古典时期的希腊人将拱从他们的大部分严肃建筑中摒除，转而使用石制的梁或门楣。在这些梁中，拉应力较高，且常常逼近安全极限。即使在古代，这些柱顶过梁中也有相当一部分会开裂。这便是为什么铁筋会被用于大理石梁，比如卫城山门。挽救多立克柱式神庙并使之免于结构性坍塌的是既短又粗的石梁，当开裂时它们会转变成拱（见图9-19、插图8和插图23）。(www.xing528.com)

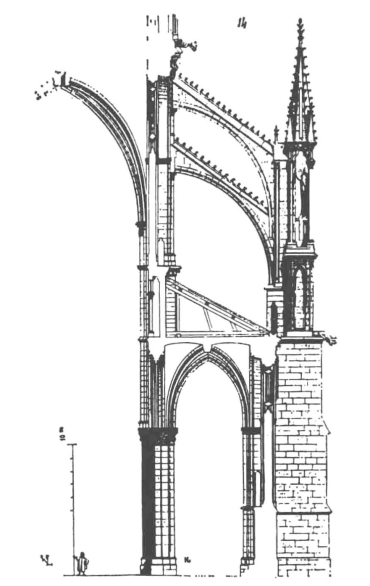
图9-18　兰斯大教堂：飞扶壁（经维奥莱-勒-杜克修繕后）

希腊横梁式（trabeate）^[11]建筑需要用到非常大的石块。随着文明的衰落，大质量石块的运输变得日益困难，这可能是个特别实际的理由，解释了为什么中世纪的建筑工匠偏爱哥特式的拱和拱顶，它们都是用相当小的石块构建的。

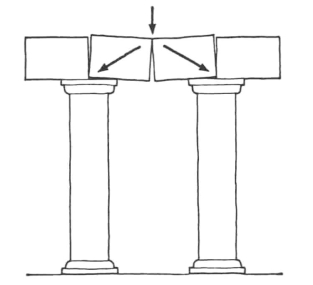
图9-19　如果短的石门楣或柱顶过梁在承张面开裂，它会自行转变为有三个铰接点的拱，并继续支撑载荷

就像大约200年前约翰·索安爵士（Sir John Soane）在他的建筑学讲座中指出的那样，虽然石梁有局限性，但古代建筑物的规模往往大于相应的现代建筑物。例如，帕提侬神庙就比伦敦圣马丁教堂大得多。尽管如此，帕提侬神庙——约230英尺乘以100英尺（69米乘以30米）——与它附近的哈德良皇帝统治时期建造的奥林匹亚宙斯神庙（见插图8）相比仍是小的，后者的规模据测为359英尺乘以173英尺（108米乘以52米），能填满大半个特拉法尔加广场。但宙斯神庙在远高于它的雅典卫城的城墙面前，也不免相形见绌。此外，就纯粹的尺寸而言，许多的罗马桥梁和沟渠以任何标准衡量，都令人印象深刻。

这些古代构造更多是毁于人祸而非天灾，它们中的一些至今仍状况良好。但是，在所有这些作品中，古人或多或少都会因循旧例；当他们不能这样做时，便很容易束手无策。在现代人眼中，不仅老式的船舶和车辆几乎弱小得可怜，新式和非传统建筑物，比如古罗马的公寓楼——高大的多层住宅，也以令人沮丧的频率倒塌，以至于奥古斯都皇帝被迫颁布法令将它们的高度限制在60英尺（18米）以下。