这高屋的面目多么可敬,
古老的柱脚撑着它们的大理石屋顶,
高高支起它沉重的穹隆,
是它自己的重量成就了坚而不动,
视之宁静。敬畏与恐惧袭来,
使我满目灼痛。
——威廉·康格里夫(William Congreve),《服丧的新娘》(The Mourning Bride)
安妮女王时代只有一种文化,而且毫无疑问,康格里夫曾同戏剧作家兼布莱尼姆宫的设计者范布勒(Vanbrugh)把酒言欢,还和克里斯托弗·雷恩爵士推杯换盏。所有这些人都非常清楚,一般来说,阻止建筑物倾倒和坍塌的与其说是石块和砂浆的强度,不如说是作用于正确地方的材料重量。
然而,以一种一般方式意识到这一点是一回事,理解具体发生了什么并能预测建筑物安全与否又是另外一回事。为了对砖石结构的行为有一个恰当的科学认知,我们可以把它当作一种弹性材料,也就是说,我们必须考虑这样一个事实:石块在负载时会发生挠度变形且遵循胡克定律。虽然可能并非绝对必要,但利用应力和应变的概念也会有相当大的帮助。
当然,乍看之下,固体的砖块和石块在建筑物的载荷作用下挠度变形到任何显著的程度是不可能的。事实上,在胡克时代之后至少一个世纪的时间里,常识性观点占据了优势地位,建筑工人、建筑师和工程师坚持无视胡克定律并把砖石建筑视为完全刚性的结构。结果,他们修建的建筑物有时会因为他们的计算错误而坍塌。
事实上,砖块和石块的弹性模量并不是特别高,如同我们能从索尔兹伯里大教堂的弯曲支柱(见插图1)上看到的,砖石建筑中的弹性运动绝不像人们猜想的那么微小。即便是在一栋普通的小房子里,墙壁也可能在其自身重量的作用下沿竖直方向弹性收缩或被压缩差不多1毫米。在大型建筑物中,这种运动自然会大得多。顺便说一下,当你觉得房子在暴风中被吹得摇摇晃晃时,这不是你的幻觉,房子的确在摇晃。帝国大厦的顶部在暴风雨中的摆动幅度约为2英尺。[3]
对砖石结构的现代分析建立在简单的胡克弹性和4个假设的基础之上,所有假设后来都得到了实践经验的证实。这4个假设是:
1.压应力很小,材料不会因受压而破碎。我们已经探讨过为何会如此。
2.由于砂浆或水泥的使用,接合处之间匹配良好,压应力被传递到整个接合区域,而不只是几个点上。
3.接合处的摩擦很强,不会因砖块或石块的相对滑动而失效。事实上,在结构坍塌前,根本不会发生滑动。
4.接合处没有有用的抗拉强度。即便砂浆碰巧在张力作用下有一定强度,亦不够可靠,且必定被忽略。
因此,砂浆的功能不是把砖块或石块“黏合”在一起,而是更均匀地传递压缩载荷。
据我所知,第一个将砖石建筑的弹性形变纳入考虑范围的人是托马斯·杨。托马斯·杨思考的问题是:当不得不承受垂直压缩载荷(P)时,像墙壁这样的矩形砖石结构中会发生什么?在下文中,我简化了托马斯·杨的论证,并将之“翻译”成应力与应变的语言,当然这些术语在他那个时代是不存在的。
只要P沿中线对称作用于墙体,即向下穿过墙中央,砖石结构就会被均匀地压缩。而且,根据胡克的理论,横穿墙厚度的压应力是均匀分布的(见图9-1)。
现在假设垂直载荷P变得有点儿偏离中心,也就是说,它不再严格地沿中线作用于墙体;那么,压应力也不再均匀分布,必定是一边高于另一边,以便对载荷做出适当反应并保持平衡。如果材料遵循胡克定律,那么托马斯·杨就认为应力应呈线性分布,如图9-2所示。
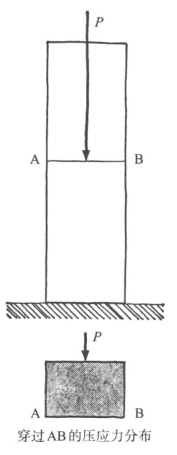
图9-1 作用于接合处AB中心的载荷P

图9-2 载荷P略偏离中心但作用于AB的“中间三分之一”以内的区域
到目前为止,接合处的砂浆完好无损,因为整个接合宽度在压缩状态下仍然是安全的。但是,若负载位置离中心更远——事实上,到了墙壁“中间三分之一”的边缘处——则会出现如图9-3所示的情况,载荷分布呈三角形,接合处外缘的压应力为零。
这本身不太重要,但对预计有事会发生的人来说,它必定变得越来越明显了。事实上,如果载荷现在向外偏离得更远一点儿,就会有事发生,如图9-4所示。
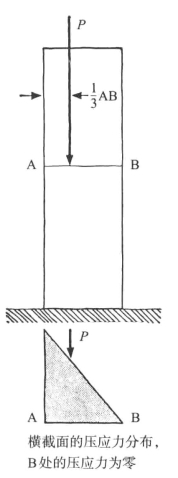
图9-3 截荷P作用于AB“中间三分之一”的边缘处
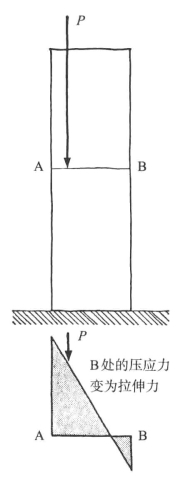
图9-4 载荷P作用于AB“中间三分之一”以外的区域(https://www.xing528.com)
墙另一面的应力现在会从压力变成张力。然而,我们说过不能依靠砂浆来承受张力,这通常是十分确定的事。预期发生的事通常就是会发生:接合处裂开了。当然,墙壁开裂是件坏事,在井然有序的建筑物里这种事情是不应该也不允许发生的,但它不一定会导致墙壁立即坍塌。现实生活中可能发生的事情往往是,裂缝会张开一点儿,但也会依靠其他仍处于接触状态的部分继续竖立在那里(见图9-5)。
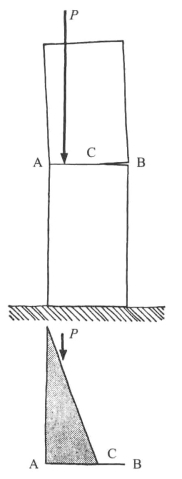
图9-5 真正发生的事情,即图9-4所示情况的结果。B到C的接合处开裂,载荷被转移到AC区域——等效于一堵更窄的墙
这一切多少有点儿危机四伏的感觉,总有一天推力作用线可能会离开墙壁表面,到那时候,稍微想想就能明白,因为没有张力的作用,一个或多个接合处会绕其外缘转动,导致墙壁倾倒和坍塌(见图9-6)。真的会这样。
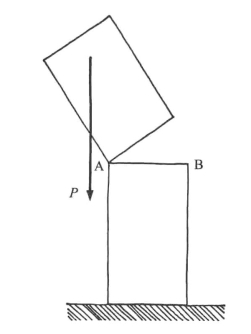
图9-6 当载荷P的作用越过A,即到达墙面以外时,墙会绕A转动,倾倒和坍塌
托马斯·杨大约是在1802年得出了这些结论,那时只有29岁的他被任命为伦敦皇家研究院的自然哲学讲席教授。同一年,他的同事——在某种意义上也是他的对手——汉弗莱·戴维在24岁这个不可能的年纪被任命为化学教授。当时和现在一样,皇家研究院的教授循例要为大众开设系列讲座。而且,这些讲座颇具电视节目的特色,皇家研究院在经费和宣传上都严重依赖这些讲座。
托马斯·杨对待自己的教育使命十分认真,他满怀探索的热忱,开设了有关各种结构弹性的系列讲座,对墙和拱的行为做出了许多有用且新颖的观察。
那时候,到阿尔贝马勒街听讲座是一种很时髦的行为,据说听众中大部分是“愚妇和半吊子哲学家”。但托马斯·杨丝毫不会怠慢女性听众,他在演讲的开场白里说:
为我的大部分听众提供知识,是我开设讲座的目的。按照文明社会的习俗,其中一种性别在某种程度上被免除了更艰辛的职责,而这份重任却占据了另一种性别的时间和精力。在上流社会中,女性的许多闲暇时光都会被利用起来,她们获得了更大的满足感,提升心智并获取知识,而非娱乐嬉戏,白白浪费空余的时间……
然而,命运并不总是眷顾那些演讲者,无论他们多么诚挚地传播有用的知识,上流社会的一些女性可能还是会悄悄溜走,宁愿无聊地打发空余的时间。不管怎样,戴维在他的讲座中展示了一些与新的电流体相关的精彩现象,还有丰富多彩的化学实验。他是个有冲劲儿的年轻人,具备我们今日所谓的电视明星的气质。戴维的形象也非常帅气,年轻女性争相参加他的讲座,因为他的演讲并不总是学术性的。某位女性听众曾说:“他那双眼睛除了凝视坩埚外,还可以用来做别的事。”就上座率而论,结果是毋庸置疑的,而我们也被告知:
托马斯·杨医生对自己讲授的主题有深刻的认识,无人胆敢置喙,同一家剧场里的同一批听众也被戴维所吸引,但托马斯·杨发现自己的拥趸数量每天都在减少,只因他的风格过于严肃和说教。
如果托马斯·杨能激起注重实用的工程师的兴趣并获得他们的支持,这类失败可能就没什么大不了的。然而,那时候工程行业的引领者甚至主宰者是了不起的托马斯·特尔福德,如我们所知,他的看法是力求实用而反对理论的。结果是,托马斯·杨立即辞去了他的讲席职位,重返医生岗位。[4]弹性研究发展多年后传到了法国,那时拿破仑正积极鼓励关于结构理论的研究。
在托马斯·杨的讲座中,令时髦女郎感到无聊的关于弹性压缩的理论、“中间三分之一”和不稳定性,几乎涵盖了我们需要知道的有关砖石结构接合处行为的一切,前提是我们也知道重量的作用位置。换言之,载荷偏离中心有多远?
最佳的确定方法就是借助所谓的“推力作用线”,即从顶部到底部沿建筑物的墙壁向下的一条直线,它定义了垂直推力在逐个接合处作用的位置。推力作用线是法国人的发明,似乎是库伦(Coulomb)最先想到的。
对于简单对称的墙、圆柱形石柱或纪念柱,如图9-7所示,推力作用线明显会向下穿过墙中心,所以没什么问题。但是,在标榜精致的建筑物里,可能至少有一个斜向力源自顶部构件的侧向推力,后者来自拱门、拱顶或各种其他形式的不对称结构。在这样一种情境中,推力作用线将不再恰好向下穿过墙中心,而会偏向一边,常常形成如图9-8所示的曲线路径。[5]

图9-7 在最简单的对称情境中,“推力作用线”向下穿过墙中心

图9-8 斜向负载的结果是以这种方式使推力作用线发生偏斜
如果我们在绘制推力作用线时发现它在任意时刻有触达墙面的危险,那么我们显然应该重新思考并深思熟虑,因为像这样的建筑物坍塌的概率很大。
我们能够做的事情之一,也可能是最有效的事情之一,就是在墙顶端增加重量。之后发生的事情如图9-9所示。与人们的想象相反,顶端的重量可能让墙具备更多而非更少的稳定性,并把偏斜的推力作用线稍微带回它应该在的地方。
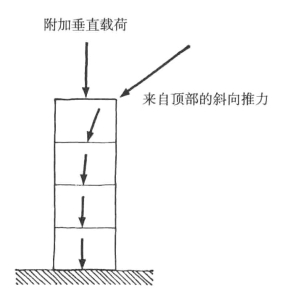
图9-9 墙顶端附加载荷的效果是减小推力作用线偏离中心的程度
方法之一就是把墙修得比实际所需更高,此外,沉重的栏杆和顶盖等也是不错的选择。如果你能负担得起成本,可以在屋顶安放一排雕像(见图9-10)。这就是哥特式教堂和主教座堂的尖顶和雕像在结构上的合理性。面对那些功能主义者和满口“效率”的无趣之人,它们真真正正地居高临下地说了声“呸”。
我们过去常强调推力作用线[6]必须维持在墙的“中间三分之一”区域内,因为如果出现裂缝,墙就有可能坍塌。这是一个合理的保守原则,它是为了安全制定的,也应该遵守,但在这个放纵的时代,恐怕很难做到。见过现代住宅区或新式大学的人,免不了看见满是裂缝的墙壁,哪里有裂缝,哪里就一定受过拉应力。然而,虽然这些裂缝对粉刷作业和内部装潢造成了很大破坏,[7]却极少对主体结构的稳定性构成任何危险。
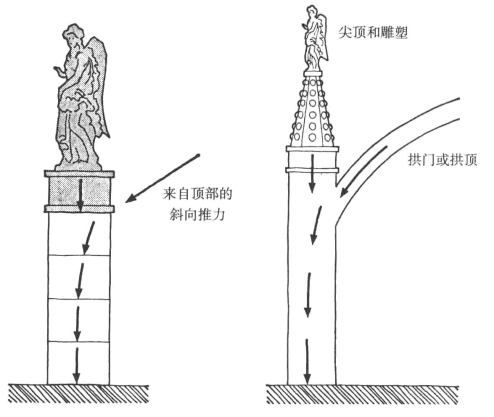
图9-10 以尖顶、雕像等形式增加顶部的重量
保证砖石建筑安全的基本条件是,推力作用线应该始终维持在墙壁或圆柱的表面以内。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




