软组织行为揭示：应力-应变曲线的真实结构

据我所知，如今的细胞壁不只是依靠直截了当的表面张力机制在运行，其中很多都在以相似的机械方式行动。简单的表面张力的难点之一在于，张力作用是恒定的，不能通过增厚皮肤来增加，这就限制了此类容器的尺寸。

但是，大自然是能够生产一种材料，使其具备“通过厚度补偿”表面张力的特性的。一个稍显尴尬的例子可能为许多人所熟知：当牙医叫你朝盆里吐口水时，唾液形成的线或带有时好像可以无限延伸而不会断。我们可能完全搞不清楚其中的分子机制，但这种材料的行为用应力和应变来表示的话，跟图8-1很像。

大部分动物组织不像唾液那样可以延展，但其中大部分的确表现出相当类似的特性，它们的应变高达50%或更多。年轻人的膀胱或多或少都会以这种方式拉伸至发生大约100%的应变，狗的膀胱可以拉伸到200%左右。如我们在第3章提到的，我的同事朱利安·文森特博士揭示出，雄性蝗虫和雌性雏蝗虫的柔软表皮仅能满足100%以下的应变，而怀孕雌性蝗虫的表皮却会伸展到1200%，且仍能完全恢复，真是太不可思议了。

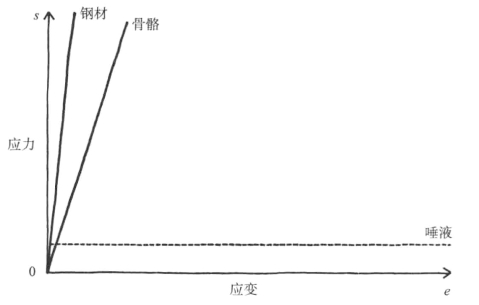
图8-1　钢材、骨骼和唾液的应力-应变曲线

虽然大部分膜和其他软组织的应力-应变曲线不是严格意义上的水平线，但通常十分接近，至少对于前50%左右的应变是这样，而且我们完全能预估这种弹性的结果是什么。事实上，任何由这种材料制成的结构必然类似于液体薄膜在表面张力作用下形成的结构，观察它们的最好办法就是在浴缸里吹肥皂泡。

这里涉及的基本原理是：这类材料或膜本质上是一种恒定应力的装置，即它只能提供一个应力，这个应力会作用在各个方向上。符合这种条件的外壳、器具或压力容器只能是球体或者球体的一部分，这在肥皂泡和啤酒沫中非常明显。如果要用这种膜做一只加长的动物，那么最佳选择似乎是“分节式”结构，如图8-2所示，事实上这种结构在蠕虫状生物中相当常见。

不论这种构造对蠕虫表皮来说有多么成功，一旦需要像血管这样的管状物，它就没什么用了。对管道而言，如第6章所说，周向应力必然为纵向应力的两倍，这种差异是我们已探讨的那种膜不具备的。所以，有必要找到一种材料，其应力-应变曲线如图8-3所示向上倾斜。

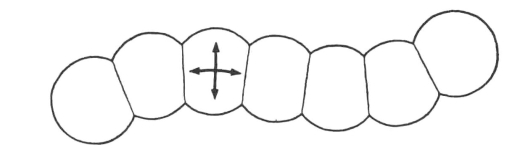
图8-2　分节式动物，其表面两个方向的应力都相等

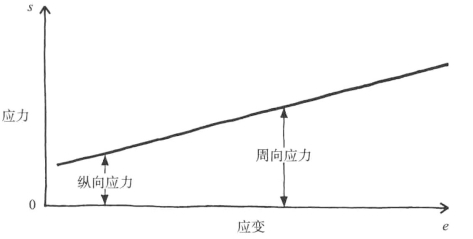
图8-3　要制造圆柱形容器的外壳，膜的应力-应变曲线必须朝上倾斜，以提供两倍于纵向应力的周向应力(www.xing528.com)

符合条件的最明显的一种高度可延展固体就是橡胶，如今有大量的橡胶类材料可用，包括天然的和人工的；其中一些的应变可延伸到800%左右，它们被材料科学家称为“弹性体”。我们把橡胶管用于各种技术目的，可以设想大自然的义务便是进化出适合构成静脉和动脉的橡胶态固体。但这恰恰是大自然没做过的事情，而且结果表明，它有一个充分的理由。

橡胶类材料的应力-应变曲线呈现出非常独特的“西格玛”形或“S”形（见图8-4）。凭借我那不太扎实的数学功底，我推断出，如果我们用这种材料制成管道或圆柱并向里面充气，借助内压产生50%或更多的周向应变，那么这个膨胀过程会变得不稳定，管道会凸起，就像一条吞下一个足球的蛇，形成球状突出物，即医生描述的“动脉瘤”。由于通过普通的圆柱形儿童橡胶气球（插图3）的爆炸实验就可轻易地得到该结果，所以我的数学推导可能是对的。

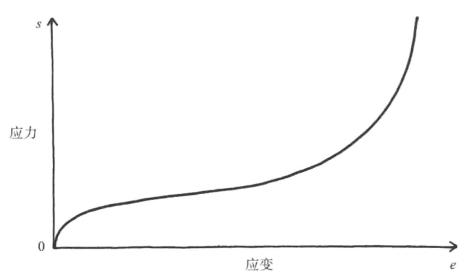
图8-4　橡胶类材料的典型应力-应变曲线

由于静脉和动脉通常的应变为50%左右，而且就像任何医生都会告诉你的那样，血管中最需要避免的情况之一便是血管瘤的产生，所以任何一种橡胶弹性都不适于我们体内的大部分膜；事实上，它在动物组织中相当罕见。

我们的数学推导结果表明，在高应变的情况下，唯一一种在流体压强作用下完全保持稳定的弹性如图8-5所示。稍做变化，这种应力-应变曲线在动物组织尤其是膜中，其实非常普遍。如果你拉一拉自己的耳垂，就能感受到确实如此。

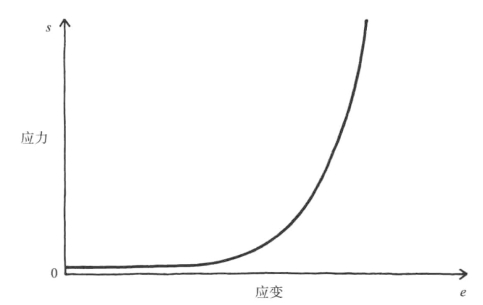
图8-5　动物组织的典型应力-应变曲线

注意，图8-5似乎回避了一个问题，即这种材料的应力-应变曲线是否会通过原点（应力和应变皆为零的点），或者在无应变时材料中是否仍存在有限的张力。如果像钢材这样的胡克材料出现该情况，毫无疑问，将会震撼工程师的灵魂。但是，在人所能见的活体范围内，似乎没有什么材料真正对应于“原点”，即显然不存在应力和应变皆为零的真实状态，如同肥皂薄膜构成的任意结构那样。至少动脉在体内始终处于紧张状态，如果把它们从活体或刚死亡的动物身上解剖出来，它们会明显地缩短。

如我们将在下文看到的，这种紧张或许是一种附加手段，用于抵消动脉随血压变化而改变长度的趋势；或者它可能代表一种迟来的尝试，以平衡动脉壁内的纵向应力和周向应力。换言之，这是一种恢复某种表面张力状态的尝试，该状态可能存在于模糊的过去。当人们经历剧烈且持续的振动（例如，守林员使用链锯的情况）时，这种紧张可能会消失，而动脉会伸长并形成一条蜿蜒、盘旋或曲折的路径。