格里菲斯理论揭示了临界格里菲斯裂缝长度

对船尾推进轴来说，晃晃荡荡总比表面有裂缝好。

——鲁德亚德·吉卜林（Rudyard Kipling），《施面包于水上》（Bread upon the Waters，1895）

我在本章开头说过，所有工艺结构都包含裂缝、划痕、孔洞等缺陷，船舶、桥梁和机翼上容易产生各种各样的意外凹痕和磨损，而我们不得不学会尽可能安全地与之共存。但是按英格利斯的说法，其中很多缺陷处的局部应力可能已远超材料公认的断裂应力。

就在吉卡林讲述那个有关裂缝的精彩故事的25年后，格里菲斯（A.A.Griffith）在他于1920年发表的一篇论文中提出了一个问题：我们通常如何以及为何能与这些高应力在无灾变的情况下共存？因为格里菲斯当年只是个年轻人，所以几乎没人注意到他的研究。不管怎么说，格里菲斯处理断裂问题时用的是能量，而非外力和应力，这不仅在当时是新颖的，而且在此后多年间对工程思考的氛围来说也相当陌生。即便到今天，还有很多工程师不太明白格里菲斯的理论到底说了些什么。

格里菲斯说的是这样一件事。从能量的观点来看，英格利斯的应力集中不过是一种将应变能转化为断裂能的机制（好似一条拉链），就好比电动机不过是一台将电能转化为机械功的机器，或者罐头刀不过是用肌肉能量切开罐头的器械。这些机制本不会起作用，除非其持续获得合适的能量供应。应力集中发挥了很好的作用，但若要持续将材料中的原子分开，则需要应变能来维持。如果应变能的供应枯竭，断裂过程就会终止。

现在假设有一块弹性材料，拉伸后夹住它的两端，使其暂时没有机械能输入或输出。于是，我们便有了一个包含大量应变能的封闭系统。

如果一条裂缝扩展并贯穿了被拉伸的材料，那么必要的断裂功将不得不付出能量的代价，且仅限于现成的能量。为方便计算，假设我们的样品是一块单位厚度的材料板，那么要付出的能量为WL，其中W为断裂功，L为裂缝长度。注意，这是一个能量的负债，一项需记在借方的能量值，尽管事实上概不赊欠。这个借方额度的增长是线性的，或随裂缝长度L的一次幂的增加而增加。

这个能量需要立即从内部资源中获得，因为我们处理的是一个封闭的系统，它只能来源于系统内的应变能的释放。换言之，样品中某处的应力必须减小。

这是因为缝隙在应力的作用下会裂开一点儿，所以紧邻裂缝表面的材料是松弛的（见图5-11）。大致说来，两个三角区域（图中阴影部分）会释放应变能。不出所料，不论裂缝长度L是多少，这些三角区域会大致保持同样的占比，其面积会随裂缝长度平方（L2）的增加而增加。因此，应变能的释放会随L2的增加而增加。

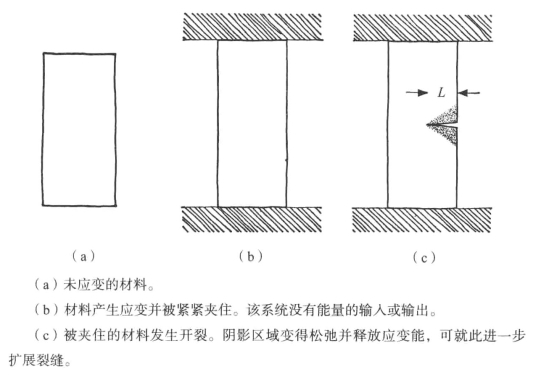
图5-11

因此，格里菲斯理论的核心是，裂缝的能量负债只随L的增加而增加，而其能量的贷方额度随L2的增加而增加。这样的结果可由图5-12形象地表示出来。OA表示随裂缝扩展而增加的能量需求，它是一条直线。OB表示随裂缝扩展而产生的能量释放，它是一条抛物线。净能量衡算为这两种效应之和，用OC代表。

在到达X点之前，整个系统都在消耗能量；过了X点，能量开始被释放出来。由此可知，存在一个临界裂缝长度，我们把它记为Lg，即“临界格里菲斯裂缝长度”。比这个长度短的裂缝是安全稳定的，且一般不会扩展；而比Lg长的裂缝则会自我扩展，且非常危险。^[13]这种裂缝在材料中会扩展得越来越快，不可避免地引发“爆炸性的”、吵闹的且令人惊慌的故障。这个结构的终结会伴随着一声巨响，而非一阵呜咽，而且很可能还有葬礼。

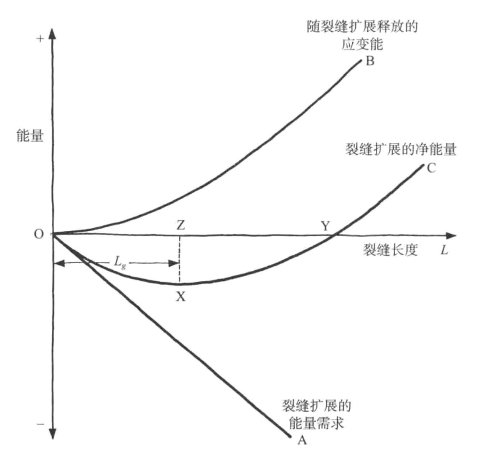
图5-12　格里菲斯能量释放，或者东西爆裂的原因

这一切最重要的后果是，即使裂缝尖端的局部应力非常高，远高于材料“公认”的抗拉强度，该结构仍然是安全的，只要没有长于临界长度Lg的裂缝或其他开口，它就不会断裂。正是这个原理使我们不致陷入对英格利斯应力集中的过度恐慌和沮丧中，也使孔洞、裂缝和划痕并不像它们看起来的那么危险。

当然，我们仍希望算出Lg的数值。结果表明，在一目了然的情况下，这比我们的任何合理预期都简单得多。虽然格里菲斯的数学推导过程可能看起来有点儿吓人，但他实际得出的结论却非常简单，因为

(www.xing528.com)

或者，用代数方法表示为，

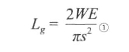
①　因为应变能为，且E = s/e，所以应变能也可写成s2/2E。

其中，W是以J/m2为单位的裂缝表面断裂功，E是以N/m2为单位的弹性模量，s是以N/m2为单位的裂缝附近材料的平均拉应力（不计应力集中），Lg是以m为单位的临界裂缝长度。（注意，这时涉及的单位是牛顿，不是兆牛顿。）

所以，一条安全裂缝的长度仅取决于断裂功与材料中存储的应变能的比值。换言之，它与“回弹性”成反比。一般说来，回弹性越强，材料能承受的裂缝长度就越短。这是鱼与熊掌不可兼得的又一个例子。

如我们所见，橡胶会存储大量的应变能。然而，其断裂功相当低，且对被拉伸的橡胶而言，其临界裂缝长度Lg也相当短，通常不超过1毫米。这就是为什么当我们拿一根针戳一个鼓胀的气球时，它会砰的一声爆炸。因此，虽然橡胶的回弹性很强且在破裂前会伸展得很长，但到破裂之时，仍像玻璃那样脆弱。

如何使回弹性与坚韧兼得，解决这个难题的一个办法是由纺织物、编织物、木制船舶和马拉车辆提供的。这些东西的接合处或多或少是松动且柔韧的，故而能量可被摩擦吸收，这也是所有咯吱咯吱声的由来。但是，纵然篱笆和鸟巢的抗攻击性较强，这种方式也不常为现代工程师所用。汽车轮胎或许是一种例外情况，原材料中加入了帆布和线绳，可使轮胎的橡胶不至于太脆。

显然，随应力s的增长，Lg会迅速缩短。因此，如果想在相当大的应力下安全地容纳一条长裂缝，那么在刚度良好（高E）的材料中，我们需要尽可能大的断裂功W。低碳钢因为兼具良好的断裂功和较高的刚度，并且相当廉价，所以获得了广泛的运用，具有很重要的经济和政治意义。

我们将会看到，虽然应用前文介绍的格里菲斯方程有许多障碍，我们也不应该视之为一种针对所有设计难题的天赐答案，但它确实为澄清曾经非常模糊且充斥着胡言乱语的各种结构状况做了很多贡献。

例如，今天的人不用再摆弄虚假的“安全系数”，就能简单地尝试设计出一个结构，使其容纳预设长度的裂缝而不断裂。选定的裂缝长度必须与结构的尺寸、可能的用途和检验环境相关。在关乎生命安全的地方，“安全”的裂缝显然要足够长，能让在周五下午的昏暗光线下心不在焉地工作的检验员看到。

在一个巨大的结构（譬如船舶或桥梁）中，为确保安全，我们可能需要它至少能承受1～2米长的裂缝。如果裂缝为1米长，我们保守地假设钢的断裂功是105J/m2，那么这样一条裂缝会一直保持稳定，直到应力达到110 MN/m2或15000 psi。然而，如果我们想要更安全，即裂缝为2米长，那么我们必须将应力减小到80 MN/m2或11000psi左右。

事实上，11000 psi只是大型结构通常的设计承受应力，而在低碳钢中，这个应力的价值是提供5～6的安全系数（严格地讲，即所谓的“应力系数”）。作为在现实中解决问题的办法，在一次对码头进行的例行检查中，4694艘船中有1289艘或者略多于1/4的船，其主体结构存在严重的裂缝——当然，事后已做补救。而实际上在海上断成两截的船的数量，大约为每500艘中有一艘，这已是相当小的比例了，但仍旧损失惨重。如果这些船的设计承受应力更大，或者用更脆的材料制造，那么在大多数情况下，直到船舶在海上出事，裂缝都不会被发现。

按照纯粹且简单的格里菲斯理论，比临界长度短的裂缝根本无法扩展，而由于所有裂缝肯定都是从短的情况开始，所以断裂应该不会发生。事实上，源于冶金学家和材料学家想出的各种好理由，小于临界长度的裂缝仍可继续扩展，如我们将在第15章看到的那样。但是，重点在于它们通常扩展得非常慢，所以我们应该有足够的时间找出它们并做出补救。

不幸的是，事情并非一直如此。格拉斯哥的船舶工程教授康恩（J.F.C.Conn）最近给我讲述了一位厨师在一艘大货轮上被吓了一跳的故事。一天早上，这位厨师走进厨舱准备做早餐，却在地板中间发现了一条巨大的裂缝。

这位厨师唤来客运主任，客运主任看后叫来了大副，大副看后又请来了船长。船长看了看裂缝说：“哦，没什么大不了的。现在我能吃早餐了吗？”

但是，厨师是个有科学家潜质的人，他吃完早餐后，便找来一些涂料在裂缝的末端做了标记，并在标记上写下了日期。下一次，当这艘船遇到坏天气时，裂缝又扩展了几英寸（1英寸=2.54厘米），厨师便涂上新标记，写下了新日期。作为一个有责任心的人，他如此做了几次。

当船最终断成两截后，厨师记录日期的那一半船体正好被打捞出水并拖回港口。康恩教授告诉我，这是对亚临界长度的巨大裂缝的扩展过程的最好和最可靠的记录。