断裂能与脆性固体强度的对比及常见材料特性

当一个固体在拉伸作用下断裂时，必须至少扩展出一条裂缝且正好贯穿材料以将其一分为二，这样至少会创造出两个在断裂前并不存在的新表面。为了用这种方法将材料撕开并生成这些新表面，需要破坏此前将两个表面结合在一起的全部化学键。

破坏大多数类型的化学键所需的能量值是众所周知的，至少对化学家来说如此。对于我们在技术上关心的大部分结构性固体，破坏任一平面或截面的所有化学键所需的总能量^[12]大同小异，约为1焦耳/平方米。

当我们处理的材料属于相当易于理解的所谓“脆性固体”（包括石头、砖块、玻璃和陶）时，该数值近似等于使这些材料断裂所需的能量值。事实上，1 J/m2的确是一个非常小的能量值。这是个发人深省的想法，基于最简单的理论，存储于1千克肌腱中的应变能足以为2500平方米（超过半英亩）碎玻璃表面的生成“买单”，这充分说明了蛮牛冲进瓷器店的后果。正因如此，砖匠用他的瓦刀轻轻一敲就能利索地把砖块一分为二，而我们只要稍不小心就会磕破盘子或玻璃杯。

当然，这也是我们要尽可能避免在拉伸状况下使用“脆性固体”的原因。这些材料是脆的，并不是因为它们的抗拉强度很低（它们破坏自身只需要很小的力），而是因为它们破坏自身只需要很小的能量。

现实中，在拉伸情况下可相对安全使用的工艺材料和生物材料，全都需要更多的能量才能生成新的断面。换言之，断裂功要比脆性固体的强度大得多。对实用的韧性材料而言，断裂功常常介于103J/m2到106J/m2之间。因此，在锻铁或低碳钢中导致断裂所需的能量，可以达到破坏玻璃或陶的等效截面所需能量的100万倍左右，尽管这两类材料的静态抗拉强度没多大差别。这就是为什么如表5-2所示的“抗拉强度”在涉及为特定用途选择材料时便颇具误导性，这也是为什么主要基于外力和应力的经典弹性理论，历经数百年的艰辛演化和教学实践的检验，却不能只靠它来预测真实材料和结构的行为。

如此巨大的能量值可被坚韧材料吸收而成为“断裂功”，虽然其详细机制往往是微妙而复杂的，但其大致原理却非常简单。脆性固体在断裂过程中所做的功，实质上仅出于破坏新断面或相邻区域化学键的需要。如我们所见，该能量很小，仅为1 J/m2左右。在韧性材料中，即使任意单独化学键的强度和能量保持一致，在断裂过程中，扰动也会波及材料精细结构的极深处。事实上，扰动的深度可达1厘米以上，即可见断面以下约5000万个原子的深度。因此，若只有1/50的原子间化学键在扰动过程中被破坏，那么断裂功——产生新断面所需的能量——会增加到百万倍，如我们所见，这正是真实发生的事情。材料内部深处的分子就是以这种方式吸收能量，并在抵抗断裂的过程中发挥作用的。

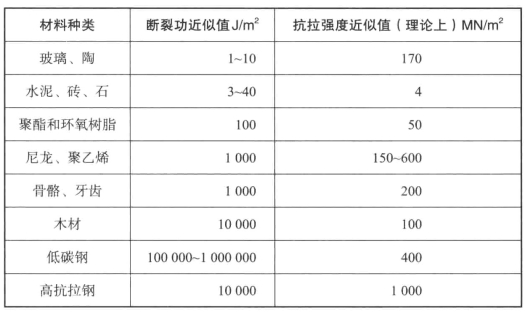
表5-2　一些常见固体的断裂功和抗拉强度的近似值

软金属的大断裂功主要归因于这些材料的可延展性。这意味着，当它们被拉伸时，其应力-应变曲线在较适中应力的作用下偏离了胡克定律，随后金属发生塑性形变，有点儿像橡皮泥（见图5-9）。当这样的金属杆或金属片在拉伸作用下断裂时，材料在像糖浆或口香糖那样断裂之前就被拉开了；其断裂末端会逐渐变尖或呈锥状，如图5-10中所示。这种断裂形式常被称作“颈缩”。(www.xing528.com)

颈缩及类似的延展性断裂之所以发生，是因为金属晶体中的大量原子层可借助“位错排”相对滑动。位错不仅能让原子层像一副纸牌那样相对滑动，还能吸收相当多的能量。在晶体中，所有这些松动、滑动和拉伸的结果都是使金属变形并消耗大量能量。

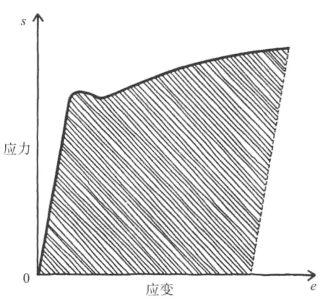
图5-9　低碳钢等可延展金属的典型应力-应变曲线。阴影区域的面积大小与金属断裂功有关

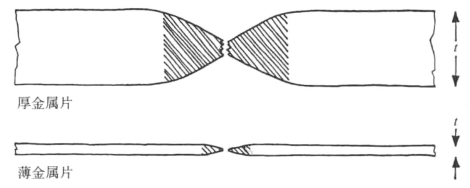
图5-10　断裂功与金属发生塑性形变的体积（阴影区域）成正比，即大致与t2成正比。因此，薄金属片的断裂功可能非常小

位错排最初是由杰弗里·泰勒爵士（Sir Geoffrey Taylor）于1934年提出的，近30年来一直是学术研究的热门课题。结果表明，这是件极其微妙而复杂的事情。像一块金属这样看似简单的东西内部发生的事情，似乎与活体生物组织中的很多机制一样巧妙。有趣的是，这种巧妙的机制不可能是有意为之；可以说大自然从中一无所获，它从未在任何结构上使用过金属，金属在任何天然情况下也极少以单质形态出现。不管怎样，金属中的位错对工程师大有裨益，而且可能就是因其好处才被创造出来，它们不仅会使金属变得坚韧，还能使它们可被锻造、加工和硬化。

人造塑料和纤维复合材料有其他断裂功机制，与金属存在很大不同，但相当有效。生物材料似乎已经演化出获得高断裂功的巧妙方法，比如，在木材中就格外有效。木头的断裂功在重量相同的条件下，要优于大部分钢材。

现在，让我们继续探讨回弹性结构中的应变能如何转化为断裂功。如果你乐意，也可以说成，让我们讨论一下东西损坏的真正原因是什么。