要理解这类问题,最重要的不是做耗资巨大的全尺寸结构实验,而是进行理论分析。1913年,英格利斯(C.E.Inglis)——后来的剑桥工程学教授,与“坐而论道的教员”截然不同——在《船舶工程师学会学报》上发表了一篇论文,引发了更广泛的讨论和应用,而不仅限于船舶的强度。
英格利斯希望告诉弹性研究者的事与索尔兹伯里勋爵(Lord Salisbury)对政客说的话几乎一样,即只用小比例地图是个严重的错误。近一个世纪以来,弹性研究者一直满足于用宽泛、大致或拿破仑式的术语绘制应力分布图。英格利斯表明,这种方法只适用于表面光滑且没有形状突变的材料和结构。
几何上的不规则性,比如孔洞、裂缝和尖锐边角,之前被忽视了,但实际上,它们会显著提高局部应力——通常分布在一个非常小的区域内。因此,孔洞和沟槽可能导致其相邻区域的应力比该材料的断裂应力大得多,即便周边区域应力的总体水平很低且根据计算该结构可能是安全的。
当然,从某种意义上说,在巧克力块上刻槽及在邮票和其他纸张上打孔的人都知道这个事实。一个裁缝在撕开一块布之前,会先在其边缘剪出一个“口子”。然而,严肃的工程师对这类断裂现象没有多大兴趣,没有考虑将其归为“严格意义”上的工程学问题。
不连续固体中的任何孔洞、裂缝或凹陷,几乎都会导致局部应力的增加,这很容易解释。图4-1(a)显示了一段光滑均匀的木棒受到一个均匀的拉应力s的作用。穿过材料的虚线表示所谓的“应力作用线”,即应力从一个分子传递到下一个分子的典型路径。当然,在这种情况下,它们是一组间隔均匀的平行线。
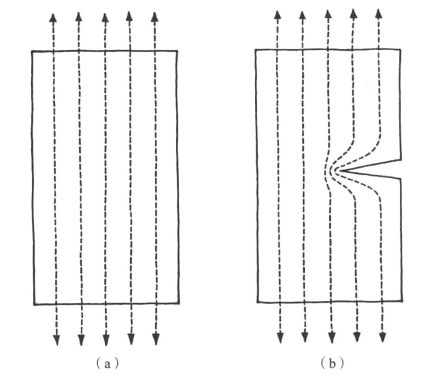
图4-1 在均匀拉伸的载荷下,无裂缝(a)和有裂缝(b)的木条上的应力作用线
如果我们现在通过在材料上制造一个切口、裂缝或孔洞来阻碍某些应力作用线,这些作用线代表的力为保持平衡就需要以某种方式做出反应。实际发生的事情与人们想象的多少有些相同:力不得不绕过缺口,应力作用线的聚集程度主要取决于孔洞的形状[见图4-1(b)]。例如,如果裂缝较长,那么裂缝尖端附近的应力作用线往往异常密集。因此在其相邻区域,单位面积上的力更大,局部应力也更大(插图2)。
英格利斯算出了遵循胡克定律的固体上一个椭圆孔洞的尖端处的应力增加量。[6]他的计算不只对椭圆孔洞是严格正确的,用于其他形状的开口也足够精确。因此,其结果不仅适用于船舶、飞机等类似结构中的舷孔、舱门和舱口,还可用于各种其他材料和装置中的裂缝、划痕和孔洞,例如牙齿填充物。
根据简单的代数运算,英格利斯说,若我们有一块材料受到远场应力s的作用,我们在其上制造一个任意形状、长度或深度为L、尖端半径为r的沟槽、裂缝或凹陷,它的尖端及其相邻处的应力就不再是s,而是增加为:
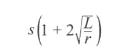
所以,对半圆沟槽或圆孔洞而言(r=L),其应力值为3s;但对像舱门和舱口这样常有尖锐边角的开口来说,r会很小而L会很大,所以边角处的应力可能非常大,足以让船舶断成两截。
在狼号驱逐舰实验中,引伸计或应变仪被夹在舰船镀层的不同位置。借助这些仪器,我们可以读出钢板的伸长量或弹性运动。据此,钢板的应变和应力就很容易计算出来了。巧合的是,没有一个引伸计被置于靠近舱口或其他开口的边角处。如果这样做,当船扎进波特兰岛大潮的浪头时,肯定能取得一些非常惊人的读数。
当我们从舱口转向裂缝时,情况变得更糟了,因为裂缝长度通常为厘米乃至米的量级,而其尖端半径可达到分子尺度——小于百万分之一厘米,这使得 非常大。因此,裂缝尖端处的应力很可能是材料中其他地方应力的上百倍,甚至上千倍。
非常大。因此,裂缝尖端处的应力很可能是材料中其他地方应力的上百倍,甚至上千倍。
如果英格利斯的结果完全按其表面意义取值,那么我们根本不可能造出一个安全的张拉结构。事实上,在拉伸状态下实际使用的材料,如金属、木材、绳索、玻璃纤维、织物以及大部分生物材料,都很坚韧。这意味着,它们或多或少会具备某种精妙的机制来抵御应力集中的效应,我们将在下一章中讨论这个问题。然而,即便在最好、最坚韧的材料中,这种防护也是相对的,而每种张拉结构在某种程度上都是敏感的。
但是,像玻璃、石头和混凝土等“脆性固体”,则没有这种防护机制。换言之,它们相当符合英格利斯在计算中所做的假设。而且,我们不需要人为制造可增加应力的沟槽来弱化这些材料。大自然已经慷慨地为我们准备了,在我们用它们来搭建结构之前,真实的固体几乎总是遍布各种微小的孔洞、裂缝和划痕。(https://www.xing528.com)
基于这些原因,在承受相当大的拉应力的情况下,使用任何脆性固体的行为都是轻率之举。当然,它们在砖石建筑、道路等领域应用广泛,但至少应在承压状态下。有时我们无法避免一定的张力,例如在玻璃窗中,我们既要小心维持非常小的拉应力,还得应用一个较大的安全系数。
谈到应力集中,我们务必注意,弱化效应并不完全是由孔洞、裂缝及其他材料缺陷造成的。附加材料也可以导致应力集中,前提是这样做诱发了局部刚度的突增。因此,如果我们在旧衣服上打块新补丁,或者在军舰的薄弱处加装护甲板,是不会有好结果的。[7]
原因在于,像强劲的补了这样小的应变区域造成的应力作用线转移,同像孔洞这样大的应变区域造成的应力作用线转移的效应差不多。可以说,弹性与结构的其余部分不协调的任何材料都会导致应力集中,并可能带来危险。
当我们试图通过附加材料来“强化”某物时,务必要小心,不要适得其反。据我的经验,受雇于保险公司和政府部门的检验员,若坚持通过安装加固件和加固套“强化”压力容器和其他结构,有时就可能引发他们试图防止的事故。
大自然通常很擅长规避这种或那种应力集中。但是,有人认为应力集中对于骨科手术意义重大,尤其是在外科大夫把强劲的金属假体安装到柔韧的骨头上时。
(注:在英格利斯的公式中,L是裂缝从材料表面向内延伸的长度,如果裂缝在材料内部,则取其长度的一半。)
【注释】
[1]The Double Helix,by James D.Watson,Weidenfeld & Nicolson,1968.
[2]这个过程也起着反作用;航天员在太空中经历一段时间的失重后,骨骼会因钙质流失而变得更脆弱。
[3]法国的索菲·热尔曼(Sophie Germain)可能是唯一一位在弹性领域取得成就的女性。与此相关的是,这一时期最具高等教育背景和理论头脑的两位工程师——马可·布鲁内尔爵士(Sir Marc Brunel)和他的儿子伊桑巴德·金德姆·布鲁内尔(Isambard Kingdom Brunel)都是法裔。
[4]无视数学的英国传统靠19世纪一群杰出的工程师传承不绝,尤其是亨利·罗伊斯爵士(Sir Henry Royce),他造出了“世界上最好的轿车”。
[5]1910年,在蒸汽机车的连杆设计中,安全因数至少要达到18。
[6]事实上,在拉伸作用下一块板上的一个圆孔洞的应力效应,已由德国的基尔希(Kisch)于1898年算出,而椭圆孔洞的应力效应已由俄国的克罗索夫(Kolosoff)于1910年算出。但据我所知,这些结果在英语区的船舶工业领域几乎没有引起注意。
[7]1813—1832年英国海军测量师罗伯特·赛平斯爵士(Sir Robert Seppings)曾说:“局部强化导致整体弱化。”
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




