弹性模量及其测量方法

常见生物材料和工程材料的弹性模量值可见表3-1：从怀孕蝗虫的表皮（其值很低，但对生物材料而言，不算特别低；顺便说一下，雄性蝗虫和雌性蝗虫幼虫的表皮都很强劲）起，弹性模量按升序排列，直至钻石。我们将看到，在刚度变化区间内，上限与下限之比大到6000000。我们将在第8章中探讨其中的原因。

表3-1　各种固体的弹性模量的近似值

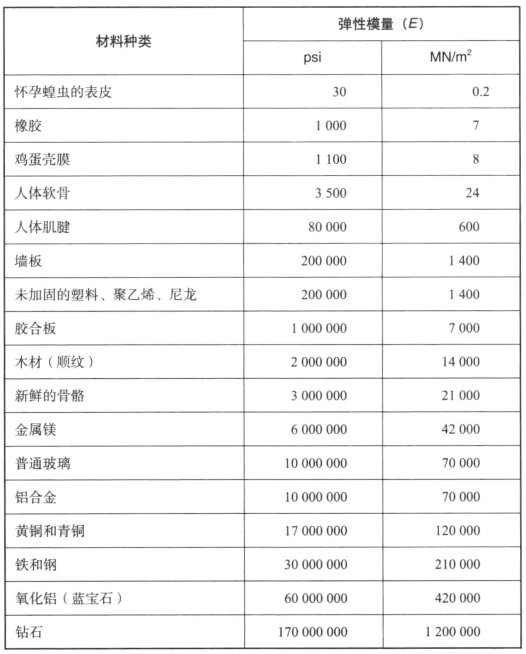
表格来源：By courtesy of Dr Julian Vincent，Department of Zoology，University of Reading.

值得注意的是，许多常见的柔性生物材料都不在上表中。这是因为它们的弹性行为即便近似，也不遵循胡克定律，所以在我们使用的术语体系中，实在没法定义它们的弹性模量。我们稍后再来讨论这类弹性问题。

如今，弹性模量被视为一个相当基本的概念；它已完全渗入工程学与材料科学领域，并开始向生物学领域进军。然而，最初历经了整个19世纪上半叶的时间，这个概念才在工程师的脑海中留下了些许印象。部分原因在于纯粹的保守主义，还有部分原因是应力和应变的概念来得太迟了。(www.xing528.com)

有了这些概念，弹性模量就变得更简单也更直观了；离开了它们，有些东西理解起来将非常困难。托马斯·杨在对埃及象形文字的解读方面扮演了重要角色，他拥有同时代人中最聪慧的头脑，但也身陷一场最严酷的智力斗争之中。

1800年前后，他用了一种与我们刚才介绍的截然不同的方法来应对这一难题，他依靠的是“比模量”的概念，即一段柱状材料在其自身重量的作用下会缩短多少。托马斯·杨于1807年给弹性模量下了定义：“任意材料的弹性模量是指同一材料的一段柱体对其底部产生的压力与造成某一压缩量的重量之比等于该材料长度与长度缩短量之比。”^[4]

相较而言，埃及象形文字也显得简单多了。

一位同时代的人这样评价托马斯·杨：“他的措辞不是人们惯用的，也常常词不达意。因此，在知识交流方面，他比我认识的任何人都逊色。”尽管如此，我们务必明白托马斯·杨是在缺少应变和应力的定义的前提下表述了一个极其复杂的概念，而那两个概念直到15～20年后才开始使用。法国工程师纳维叶（Navier）在1826年给出了弹性模量的现代定义（E=应力/应变），三年后托马斯·杨就去世了。作为应力和应变概念的提出者，柯西最终被法国政府授予男爵封号，他当之无愧。