为分析固废产品变异对道路工程结构性能的影响,可采用随机有限元法进行计算。有限元的一般方程为
K(b)u(b)=Q(b)
式中 K(b)——刚度矩阵;
u(b)——位移矩阵;
Q(b)——荷载矩阵;
b——系统参数,如弹性模量。
K、u、Q均以b 为函数。
将上方程在b 的均值点b 0泰勒展开。泰勒在b 0点展开的一般形式为:
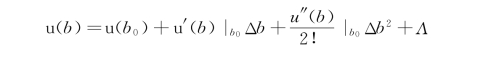
式中 Δb=b-b 0。假设Δb很小,将K、u、Q围绕b 0二阶截尾泰勒展开,得到
(K0+K′Δb+0.5K″Δb 2)(u0+u′Δb+0.5u″Δb 2)=Q0+Q′Δb+0.5Q″Δb 2
展开公式左手侧,集合同阶项,给出了一组三个公式,从中获取u0、u′、u″数值如下:
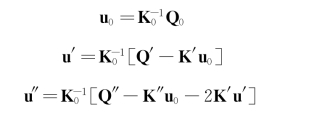
K和Q的微分通过其每一个分量对b的微分定义。
鉴于u的截尾泰勒展开,位移的预期值矢量和协方差矩阵由下式给出:
E[u]=u0+0.5u″var(b)
cov(u)=(u′)var(b)(u′)t
式中 (u′)t——u′的转置。
对于一组p 个随机变量的情况,以及一个确定荷载,上公式变为以下形式:(https://www.xing528.com)
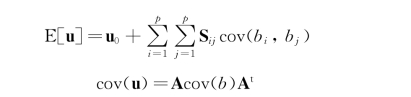
其中
![]()
式中 cov(b)——一组随机变量b的协方差矩阵,cov(bi,bj)代表了这一矩阵的一个成员;
cov(u)——随机位移的协方差矩阵。单引号边上的下标bi指关于bi的偏微分;
A——n×p 的矩阵,由p 个列矢量组成,定义为
![]()
A t——其转置;
参数n——自由度数。
图5-10给出了一个计算示例。图中hb为基层厚度,eb为基层弹性模量,Vb为基层泊松比,CV为变异系数。铺装、基层、路基中弹性模量的变异系数均为10%,但铺装层变异时,取基层、路基不变异,基层变异或路基变异时类似。可以看到,路基的变异对路表弯沉的变异影响最大,而且越远离荷载,变异性越强。而基层与铺装变异则小得多,并且离开荷载迅速衰减。
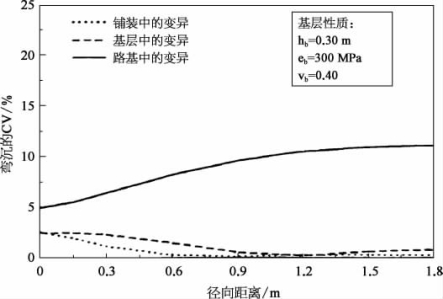
图5-10 三层铺装模型的弯沉CV(静态)(Mehdi Parvini,1997)
这一随机有限元模型应用于包含固废的道路结构,需要就以下客观情况加以考虑:
(1)上面推导中,采用二阶的泰勒截尾展开,一般来说,适用于变异系数小于30%的情况。当变异系数更大时,应考虑更高阶的泰勒展开。
(2)上面推导中,采用的是静态模型,实际道路的受力为动力学方程所控制,因此,应结合动力学参数重构方程。
(3)这里采用了弯沉作为控制指标,但目前新的道路设计规范,以沥青层层底拉应变和路基顶面压应变(如为半刚性基层),还包括基层底面拉应力为设计指标,因此应研究参数变异对这些指标的影响。
(4)利用FWD的弯沉测试结果实施道路反演计算时,应考虑各变量变异对弯沉变异的敏感性,尽可能选择敏感性小的参数。
(5)应研究固废性质变异对材料疲劳性能的影响,并结合随机有限元模型分析如何面向疲劳控制材料的相关变异性。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




