几何概率问题—《概率论（第2版）》

与古典等可能性类似的是几何等可能性.在一个线段上随机地任取一个点，那么可能的结果是线段上的所有点全体Ω，它是一个无限元素的集合，故而等可能性不能如古典情形那样用元素个数描述.重新体会随机的含义，这里所说的随机是指每个点是等可能的，但在这种情况下谈论点是没有意义的，因此我们把随机理解成为一个点落在区间I的概率只与区间的长度有关，而与其位置无关.这意味着概率与区间的长度成比例.类似地，在一个有界平面区域Ω上随机地任取一个点，落在子区域D中的概率等于子区域的面积|D|与整个区域面积|Ω|的比，类似于古典概型的定义，也就是说

这在直观上是显然的.下面是几个经典问题，也是非常直观的.

例1.4.1（约会问题）设有甲，乙两人约定8：00到9：00在某处见面，再约定先到的人只等待15分钟后离开，问两人能见面的概率是多少？在这个问题中，一个隐含的假设是他们在约定时间段的任何时间抵达的可能性都是一样的，也就是等可能性.用x，y分别表示甲乙两人抵达的时间，由于随机性，两人抵达的时间相当于在平面区域Ω={（x，y）：8≤x，y≤9}中随机地取一个点，而两人能见面这个事件相当于这个点落在区域内.它的概率就等于这个集合的面积与整个样本空间的面积的比，即7/16.

例1.4.2（Bertrand）在一个圆周上随机地任取一根弦，求其长度大于内接等边三角形边长的概率.这个问题在历史上曾称为Bertrand悖论，因为问题有不同的答案.但随着理论的完善，人们认识到导致不同答案的原因是问题中随机性的含义不清楚，或者说因为对随机性有不同的理解.所以后来称之为Bertrand奇论，它是帮助理解概率论中随机性的很好的例子.在这个问题里，随机性至少有三种理解：

（1）先在圆周上取定一点A，然后再在圆周上随机地取一个点B，连接A与B成为弦；

（2）先取定一条直径A，然后在直径上随机地取一个点B作一条过此点与直径垂直的弦；

（3）以圆内的任何点作为中点的弦是唯一决定的，因此以这个对应，随机地取一条弦就等同于随机地在圆内取一个点B.

说这三种随机性不同是说如果按（1）随机地取弦AB，那么它与圆心的距离就不可能是在半径上等可能的，它的中点也不会等可能地出现在圆内.关于此，在后面会有进一步解释.

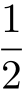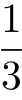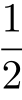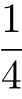一条弦长大于圆的内接等边三角形边长当且仅当弦的中点与圆心的距离小于的半径长，那么在（1）的情况下，点B必须落在点A对面的圆弧上，因此概率为，在（2）的情况下，点B必须与圆心距离不小于半径长，因此概率为，在（3）的情况下，点B必须落在半径为原来圆半径长的的圆内，因此概率为两圆面积的比.(www.xing528.com)

例1.4.3（Buあon）向一个画着等距离平行线的平面上投针，平行线间的距离为l，针的长度为a，l>a，求此针与平行线相交的概率.设针的中点与最近的平行线的距离是x，针（或其延长线）与平行线的夹角为φ，我们假设（x，φ）是在区域

上随机取的一个点（这个假设合理吗？）.事件A：针与平行线相交发生当且仅当（x，φ）落在区域因此概率是面积的比

Buあon问题还有一个漂亮的解答，不必使用积分，简述如下.设f（x）是长为x的针与平行线相交的概率，利用概率的可加性推出因此存在常数k使得对x≤l有f（x）=kx，下面我们要计算k.

f(x+y)=f(x)+f(y).

先看一个三角形扔在平面上与平行线相交的概率，同样是应用可加性，以及这样的观察：一个三角形与平行线相交当且仅当三角形的两条边和平行线相交.由此推出三角形与平行线相交的概率为

其中a，b，c是三角形三条边长.因此这个概率是周长的k/2倍.同理，任何一个直径不超过l的凸多边形随机扔在平面上与平行线相交的概率也是周长的k/2倍，取极限得一个直径不超过l的凸图形与平行线相交的概率同样如此.而一个直径为l的圆扔在平面上必然与平行线相交，即有

注意一个图形的直径是指其中最远两个点的距离.