层次分析法在多领域广泛应用

层次分析法是一种解决多目标的、系统化的、层次化的分析方法。该方法将定量分析与定性分析结合起来，用决策者的经验判断衡量目标能否实现的相对重要程度，并合理地给出每个决策方案的权重，利用权重系数得出各方案的优劣次序。目前，层次分析法的应用领域非常广泛，如工程计划、资源分配、方案排序、政策制定、性能评价、城市规划、科研评价等。

层次分析法建模的一般步骤为：

1.建立层次结构模型

应用层次分析法决策问题时，首先要把问题条理化、层次化，构造出一个有层次的结构模型。将决策的目标、考虑的因素（即决策准则）和决策对象按它们之间的相互关系分为最高层、中间层和最低层。

最高层（目标层）：分析问题的预定目标或理想结果。

中间层（准则层）：分析问题时所需考虑的准则、子准则。

最低层（方案层）：实现目标可供选择的各种措施、决策方案等。

注　层次结构模型中的层次数与问题的复杂程度及需要分析的详尽程度有关。一般地，层次数不受限制，但是每一层次中各元素所支配的元素个数尽量不要超过9个，支配元素过多会给两两比较判断带来困难。

【示例4.3.1】——大学生就业问题

大学生面临就业时，可能有学校、研究所、企业等单位可供选择，这时一般会依据工作环境、工资待遇、发展前途、住房条件等因素择业。根据以上信息，可以建立层次结构模型如下：

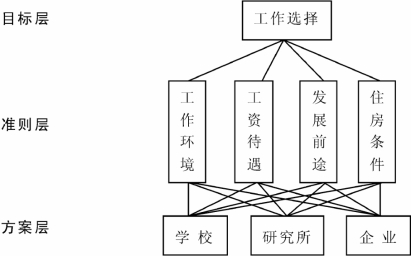
2.构造各层次的两两判断比较矩阵

层次结构反映了因素之间的关系，但各准则在目标衡量中所占的比重、不同方案对各准则的比重并不一定相同。构造两两判断比较矩阵，就是对各层各指标之间进行两两对比之后，然后排定各指标的相对优劣顺序，依次构造出评价指标的判断矩阵。

判断矩阵在构造时，所有因素按照表4.3.1所示的1～9尺度进行两两之间的对比，用aij表示第i个因素相对于第j个因素的比较结果，则。故两两判断比较矩阵A的表示为：

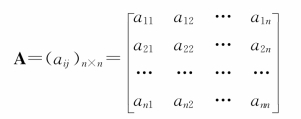
表4.3.1　比较尺度含义表

注　2，4，6，8表示第i个因素相对于第j个因素的影响介于上表两个相邻等级之间。

如在示例4.3.1中，构造第二层（准则层）对第一层（目标层）的判断比较矩阵A如下：

同样的方法构造第三层（方案层）对第二层（准则层）的判断比较矩阵B1，B2，B3。(www.xing528.com)

3.层次单排序及一致性检验

层次单排序就是确定下层各因素对上层某因素影响程度的过程。具体作法为：计算判断矩阵A对应于最大特征值λmax的特征向量W，经归一化后即为同一层次相应因素对于上层某因素相对重要性的排序权重。

对判断矩阵的一致性检验的步骤如下：

（1）计算一致性指标CI，

（2）查找相应的平均随机一致性指标RI，具体见表4.3.2；

表4.3.2　平均随机一致性指标RI

（3）计算一致性比率CR。

注　当CR＜0.10时，认为判断矩阵的一致性是可以接受的，否则要重新构造判断矩阵。

4.层次总排序及一致性检验

层次总排序就是确定最低层（方案层）对最高层（目标层）的排序权重，从而进行方案选择，总排序权重要自上而下地将准则下的权重进行合成。具体作法为：

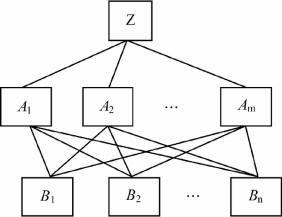
　设A层m个因素A 1，A 2，…，Am对总目标Z的排序为a 1，a 2，…，am；B层n个因素对上层A中因素为A j的层次单排序b 1j，b2j，…，bnj（j＝1，2，…，m）；B层的层次总排序（B层第i个因素对总目标的权重）为

5.层次总排序的一致性检验

设方案层各因素B 1，B 2，…，Bn对准则层中各因素A j的层次单排序一致性指标为CIj，随机一致性指标为RIj，则层次总排序的一致性比率为：

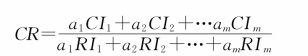
注　当CR＜0.10时，认为层次总排序通过一致性检验。