MATLAB系统聚类法-数学实验中的成果

MATLAB软件中自带了用于聚类分析的工具包，系统聚类分析中常用的函数命令及其调用格式如下：

zscore＼pdist＼squareform＼linkage＼cluster＼clustedata＼dendrogram＼corrcoef——计算聚类分析的相关结果

【语法】

bx＝zscore（x）返回样本矩阵x的标准化矩阵bx；

y＝pdist（x，′metric′）返回样本数据两两之间的距离矩阵y；参数x为样本数据，metric为距离类型，缺省时为欧氏距离。其他常用距离参数为：seuclidean（标准化欧式距离）、mahalanobis（马氏距离）、minkowski（闵可夫斯基距离）；

z＝squareform（y）返回距离矩阵y的三角阵形式z（或者方阵形式），返回类型根据输入参数类型而定；

z＝linkage（y，′method′）返回利用距离矩阵y创建的系统聚类树z，参数method为相应的算法，缺省时为最短距离法。其他常用的参数取值为：complete（最长距离法）、average（未加权平均距离法）、weighted（加权平均法）、ward（最小方差法）；

t＝cluster（z，n）返回根据系统聚类树z创建的n个类的分类情况t；

t＝clustedata（x，n）返回根据样本数据x创建的n个类的分类情况t，其结果与下列一组命令等价：［h，t］＝dendrogram（z）返回聚类谱系图；corrcoef（）返回指标之间的相关系数。

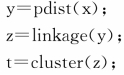
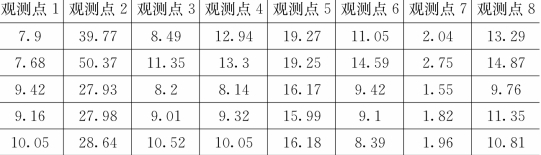
【示例4.2.1】设某地区有八个观测点的数据，样本数据矩阵见表4.2.1，根据最短距离法对表中数据进行系统聚类。

表4.2.1　八个观测点数据

命令窗口编写MATLAB代码如下：

运行后得到输出结果为：

聚类谱系图如图4.2.2所示。

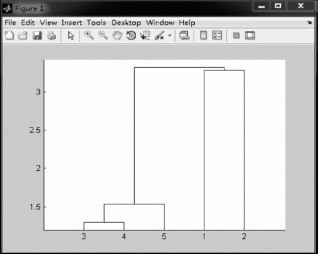
图4.2.2　八个观测点数据的聚类谱系图

根据上述结果可知，利用最短距离法分类时，1和2各是一类，3、4、5是另一类。

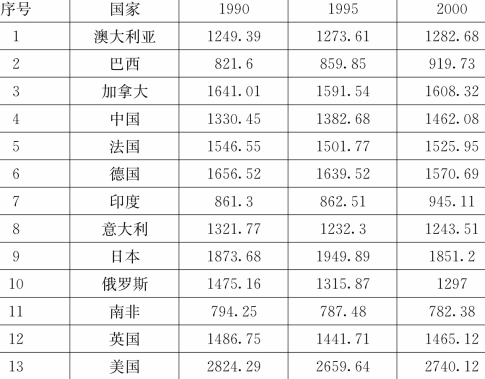
【示例4.2.2】现有13个国家1990，1995，2000年的可持续发展能力见表4.2.2，试用不同的距离指标将13个国家分为4类。

表4.2.2　13个国家可持续发展能力表(www.xing528.com)

命令窗口编写MATLAB代码如下：

运行后得到输出结果为：

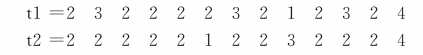
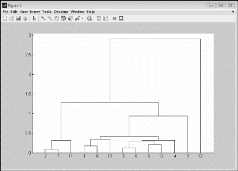
图4.2.3　基于欧式距离的聚类谱系图

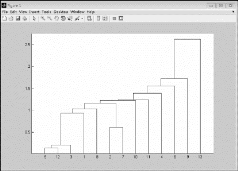
图4.2.4　基于马式距离的聚类谱系图

根据上述结果可知，13个国家分别按照欧式距离和马氏距离进行聚类分析的过程是略有不同的，具体的聚类结果见表4.2.3和表4.2.4。

表4.2.3　欧式距离的聚类情况表

表4.2.4　马式距离的聚类情况

对照表4.2.3和表4.2.4发现，两种距离下的聚类稍微有所不同，重点体现在德国、巴西、印度、南非和日本这五个国家的分类上，因而选取合理的距离准则和聚类方式是十分必要的。

【能力训练4.2】

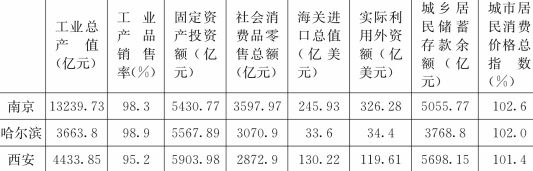
1.全国十大城市经济指标对比见表1，请按表中数据对指标进行聚类分析，将十个城市分为3类。

表1　十大城市经济指标对比表

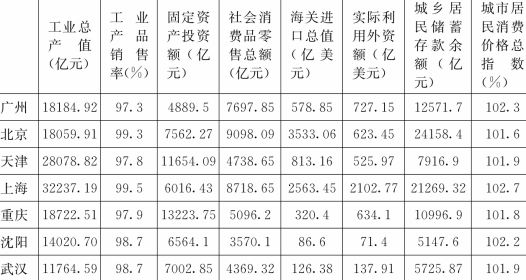
续表