优化问题应用领域广泛、种类繁多，因而分类的方法也很多。通常可以按照变量的取值特征、有无约束条件、目标函数个数等情形分类，常见的具体分类情况如下：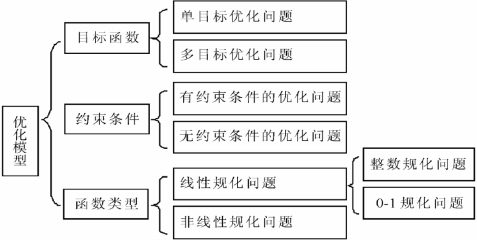
下面分别举例来介绍一下这些常见的优化模型。
1.由某实际问题确定决策变量，建立一个具有目标函数且无约束条件的求函数最大值、最小值问题的模型，称为无约束优化模型，其数学形式为：
【示例3.1.2】——无约束优化模型
计算函数z＝x 21＋2x 22－x 23＋2x 1x 2－4x 1x 3＋x 2x 3的最大值和取得最大值的点。
建立最大化优化模型为：
2.由某实际问题确定决策变量，建立一个具有目标函数和若干个约束条件（等式或不等式）的求函数最大值、最小值问题的模型，称为有约束优化模型，其数学形式为：
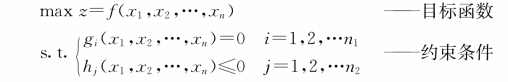
【示例3.1.3】——有约束优化模型
计算多元函数z＝x 1x 2…x n在约束条件x 1＋x 2＋…＋x n＝2017，x i≥0，i＝1，2，…，n下的最大值和最大值点。
建立最大化优化模型如下：
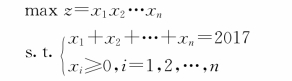
3.由某实际问题确定决策变量，建立一个决策变量为非负的，目标函数和约束条件都是变量线性函数的求函数最大值、最小值问题的模型，称为线性最优化模型，简称为线性规划模型，其数学形式为：
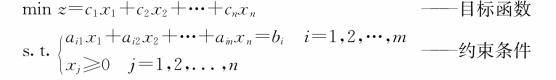
【示例3.1.4】——线性规划模型
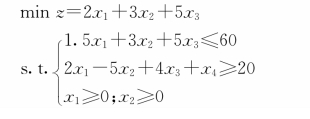
实际问题中，经常遇到两类特殊的线性规划问题，一类是所求变量要求是非负整数，称为整数规划问题；另一类是所有决策变量要求只能取0或1，称为0-1规划问题。
【示例3.1.5】——整数规划模型
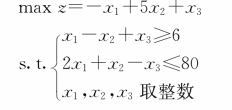
【示例3.1.6】——0-1规划模型
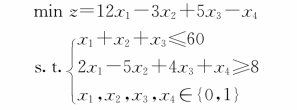(www.xing528.com)
4.由某实际问题确定决策变量，建立一个具有目标函数或约束条件表达式中有变量的非线性函数的求函数最大值、最小值问题的模型，称为非线性规划模型，其数学形式为：
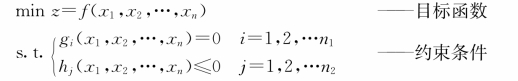
其中，目标函数f或约束条件g i中含有关于变量的非线性函数。
【示例3.1.7】——非线性规划模型
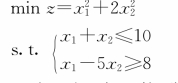
上面的几类优化模型中，只有一个目标函数，称为单目标优化模型。
5.由某实际问题设立变量，建立两个或两个以上目标函数和若干个约束条件的求函数最大值、最小值问题的模型，称为多目标优化模型，其数学形式为：
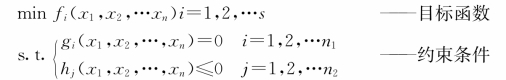
上述模型中包含s个目标函数，n 1个等式约束条件和n 2个不等式约束条件。
注 多目标优化问题一般转化为单目标优化问题求解。
【示例3.1.8】——多目标优划模型
【能力训练3.1】
1.设有两座矿山A、B，另有三个炼铁厂甲、乙、丙需要矿石，各矿山日产量和各厂日需量及对应的运价（元）见表1，请问怎样调用矿石才能使总费用最小？
表1 矿石需求量、产量表
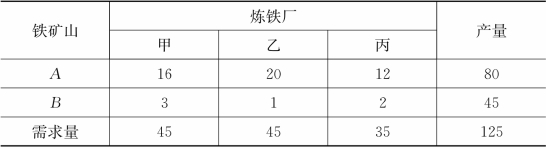
2.（投资决策问题）某企业有n个项目可以进行投资，需要至少投资1个项目，已知该企业拥有可用于投资的总资金为A元，投资第i个项目需要资金a i元，（i＝1，2，…，n），并且预计可获得收益bi元，试选择最佳的投资方案，建立优化模型，使得该企业最终获利最大。
图1 竖行海报设计图
3.学校举行活动，需要张贴海报进行宣传，现让你设计一张如图1所示的竖行海报，要求版心面积不少于130cm2，上、下两边最少各留2cm的空白，左右两边最少各留1cm空白，试设计最佳尺寸，使四周空白面积最小？
4.（多目标优化）已知某商场有A 1、A 2、A 3三种礼品，单价分别为40元/个、28元/个、34元/个。年底要筹办一次年会，要求用于买礼品的钱不超于2000元，礼品数量不少于50个且A 1，A 2两种礼品的总和不少于30个，试确定最佳的礼品购买方案？
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
