1.平面数据插值
interp1——计算平面数据插值
【语法】
y1＝interp1（x，y，x1，′method′）返回横坐标为x1的待插值点的纵坐标y1；x，y为已知的样本点数据；x1不能超出x的范围；method为插值方法，包括：nearest（最近邻点插值）、liner（线性插值）、cubic（三次Hermite插值）、spline（三次样条插值）。
注 当x1为一个数据点时，得到的是该点的函数值；当x1为一个向量或者矩阵时，得到的是相应维度的数据点的插值函数值。
【示例2.3.1】设有一组样本点见表2.3.2，试分别利用线性插值、三次Hermite插值和三次样条插值方法获得插值点x＝10.5时的函数值。
表2.3.2 样本数据点
命令窗口编写MATLAB代码如下：
运行后得到输出结果为：
根据上述结果可知，当x＝10.5时，采用线性插值、三次Hermite插值和三次样条插值得到的函数值分别为1.9950，1.9949，1.9921。
【示例2.3.2】针对表2.3.2中的样本数据，绘制散点图、线性插值函数曲线图和三次样条插值函数曲线图。
建立M-命令文件绘制插值函数曲线图，编辑窗口输入MATLAB代码如下：
保存M-命令文件，命名为chazhi.m，运行后得到输出结果如图2.3.3所示。(www.xing528.com)
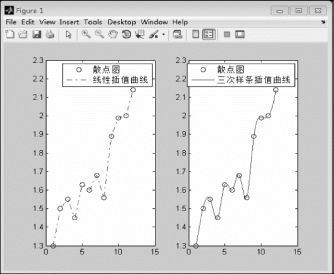
图2.3.3 数据插值图
2.网格数据插值
interp2——计算网格数据插值
【语法】
z1＝interp2（x，y，z，x1，y1，′method′）返回（x1，y1）对应的函数值z1；x，y，z为已知的样本点数据，x1，y1为用户新定义的插值点构成的网格参数，插值方法与命令interp1（）中的含义一致。
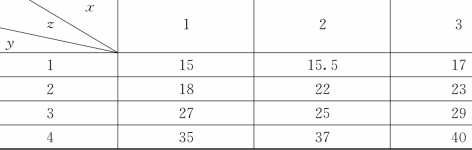
【示例2.3.3】通过抽样得到空中某飞行物体在不同时刻的位置坐标（x，y，z）见表2.3.3，试利用数据插值的方法计算该物体在地理坐标（x，y）＝（4，5）时的空中位置，并绘制该物体的运动轨迹图。
表2.3.3 不同时刻的位置坐标样本点
建立M-命令文件绘制网格数据插值函数图，编辑窗口输入MATLAB代码如下：
保存M-命令文件，命名为chazhi2.m，运行后得到输出结果为：
根据上述结果可知，该物体在地理坐标（x，y）＝（4，5）的空中位置z＝6.5000，该物体的运动轨迹图如图2.3.4所示。
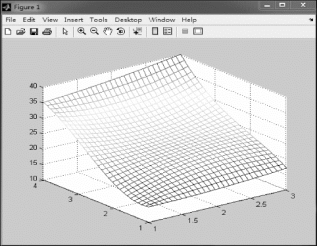
图2.3.4 网格数据插值图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
