正态分布及其性质-数学实验

normpdf＼normcdf＼normstat＼normrnd——计算正态分布的概率密度函数、分布函数、期望、方差和随机矩阵

【语法】

f＝normpdf（x，μ，σ）返回样本x的概率密度值f，正态分布均值为μ，标准差为σ；

F＝normcdf（x，μ，σ）返回样本x的分布函数值F，正态分布均值为μ，标准差为σ；

［M，V］＝normstat（μ，σ）返回均值为μ，标准差为σ正态分布的期望M与方差V；

X＝normrnd（μ，σ，m，n）返回m×n阶均值为μ，标准差为σ的正态随机矩阵X。

【示例2.1.3】分别绘制正态分布N（0，0.52），N（0，1），N（0，22）的概率密度函数和分布函数图像。

建立M-命令文件绘制概率密度函数图像，编辑窗口输入MATLAB代码如下：

保存M-命令文件，命名为normpdf1.m，运行后得到输出结果如图2.1.3所示。

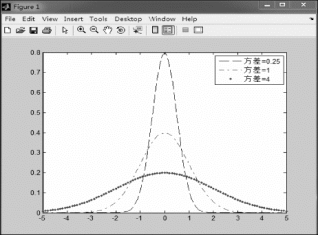
图2.1.3　N（0，σ2）的概率密度函数图像

观察图2.1.3可知，当正态分布的期望相同时，方差不同，概率密度的函数图像对称轴不变，形状在改变。方差越小，图像越瘦高，数据越集中；方差越大，图像越矮胖，数据越分散。

建立M-命令文件绘制分布函数图像，编辑窗口输入MATLAB代码如下：

保存M-命令文件，命名为normcdf1.m，运行后得到输出结果如图2.1.4所示。

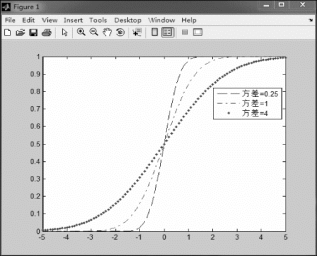
图2.1.4　N（0，σ2）的分布函数图

观察图2.1.4可知，当期望相同时，方差越小，分布函数曲线增长的越快；方差越大，分布函数曲线增长的越慢。

【示例2.1.4】按要求计算下列概率值：

（1）设X～N（2，0.52），计算P 1＝P｛0＜X＜1｝和P 2＝P｛X＜3｝。

（2）设X～N（0，1），计算P 3＝P｛－2＜X＜2｝。(www.xing528.com)

命令窗口编写MATLAB代码如下：

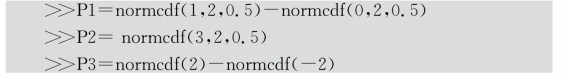
运行后得到输出结果为：

根据上述结果可知，

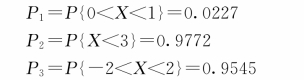
注　对于标准正态分布，计算概率密度函数和分布函数命令的调用格式也可以是normpdf（x）和normcdf（x）。

【示例2.1.5】生成100个服从正态分布N（0，1）的随机数，并绘制频率直方图。

命令窗口编写MATLAB代码如下：

运行后得到输出结果如图2.1.5所示。

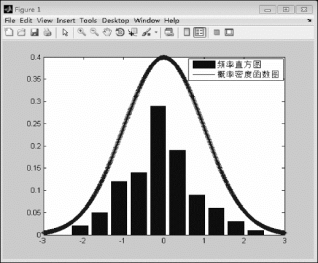
图2.1.5　正态分布随机数频率直方图

【示例2.1.6】分别生成1000个服从［0，1］上均匀分布和标准正态分布的随机数，并绘制散点图。

命令窗口编写MATLAB代码如下：

运行后得到输出结果如图2.1.6所示。

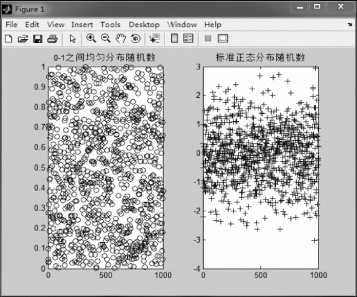
图2.1.6　均匀分布和标准正态分布随机数散点图

观察图2.1.6可知，均分分布的随机数大致均匀分散在给定区间内，而正态分布的随机数大多集中在期望的某个邻域内。