人口问题是当今世界上人们最关心的问题之一。想要预测未来某年的人口数量,需要建立相应的人口增长模型,常见的人口增长模型有马尔萨斯(Malthus)模型和罗杰斯特(Logistic)模型。
1.Malthus模型
Malthus模型又称指数增长模型,假设单位时间内人口净增长率为常数r。设t时刻人口总数为x(t),则Δt时间内增长的人口数为:
![]()
整理得
![]()
当Δt→0时,得微分方程模型
![]()
解得
![]()
其中,x 0,r为待定参数。
注 人口净增长率是人口增长数量与人口总数的比值。
【示例1.3.1】某高校在2015年底的一项统计数据显示:该校的在校学生人数以260e0.2x的速度递增,其中x=0对应2015年的学生数。若该校目前在校人数为6000人,学生宿舍为1200间,每间最多可容纳6人,试回答下列问题:
(1)预测2025年学校的在校学生数?
(2)到2025年学校最多可容纳的学生数?若不能容纳,至少还需要修建多少间宿舍?
模型假设与变量说明
(1)假设今后10年学校的在校人数均按260e0.2x的速度递增,不会出现其他变故;
(2)假设现有宿舍10年后还能正常使用;
(3)假设从2015年起的第x年该校的在校人数为P(x)。
模型的分析与建立
由题意知:![]()
利用微元法,在区间[x,x+d x]上,可将学校在校人数的增长率视为常数,增加的人数为d P=260e0.2x d x,则2025年该校在校人数为:
![]()
在命令窗口编写MATLAB代码如下:
![]()
运行后得到输出结果为:
![]()
根据上述结果可知,到2025年学校大概有学生(-1300+1300e2)人,化简后可知10年后学校将有近8306名学生。学校现有宿舍1200间,按每间最多容纳6人计,最多可容纳学生人数为:
![]()
还差床位数为:
![]()
若仍按每间6人安排,则缺宿舍数为:
![]()
即还缺185间宿舍。
2.Logistic模型
Logistic模型也称阻滞型人口模型,主要考虑到自然资源和环境对人口的影响。否定了Malthus模型中关于对净增长率为常数的假设,Logistic认为净增长率随着人口数量x(t)的增加而减小,即当x(t)→xm时,净增长率趋于零,其中xm表示自然环境条件所能容许的最大人口数(一般地,一个国家工业化程度越高,它的生活空间越大,食物就越多,从而xm就越大)。
据此,建立Logistic模型为:
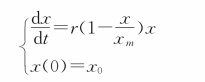
其中,r为比例系数。利用分离变量法可以得到人口数量为:
![]()
【示例1.3.2】利用Logistic模型预测世界未来人口数量。某生物学家估计,比例系数r=0.029,当人口总数为3.06×109时,人口每年以2%的速率增长,因而由Logistic模型得:
![]() (https://www.xing528.com)
(https://www.xing528.com)
即
![]()
得
![]()
即世界人口总数极限值近100亿。
【示例1.3.3】表1.3.1是美国近两个世纪的人口统计数据(百万),试建立数学模型预测2010年美国的人口数。
表1.3.1 美国人口数据
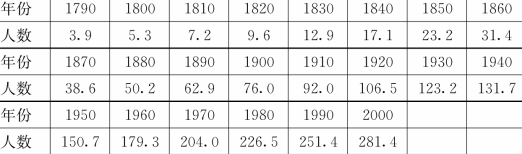
问题分析
根据题目中给定的数据,利用MATLAB软件绘制散点图,观察散点图的分布规律,确定人口模型。
在命令窗口编写MATLAB代码如下:

运行后得到输出结果如图1.3.1所示。
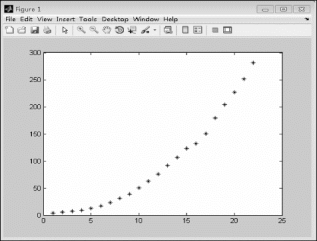
图1.3.1 美国人口数据散点图
观察散点图的走势发现,美国近两世纪的人口总数几乎呈指数形式增长,因而建立预测模型时可以选择指数模型,即Malthus模型。
模型建立
根据题意建立Malthus模型为:
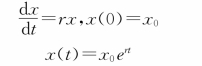
下面利用最小二乘法的非线性拟合函数进行曲线拟合,确定参数x 0,r。用1790年-1900年间的12组数据进行预测,在命令窗口编写MATLAB代码如下:

运行后得到输出结果如图1.3.2所示。

图1.3.2 美国人口数据拟合函数曲线
利用所给数据进行预测,在命令窗口编写MATLAB代码如下:

运行后得到输出结果为:
![]()
根据上述结果可知,2010年美国人口数为1168百万人,得到拟合曲线如图1.3.3所示。
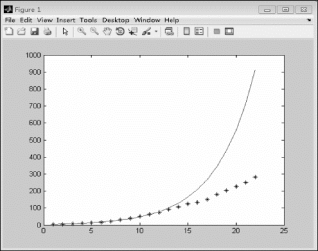
图1.3.3 美国人口数据拟合函数曲线
观察上述图像发现,前期数据比较吻合,但到后期差距就比较大,因此这个模型不能比较准确的预测人口数。
观察表1.3.1中美国人口数据,定义人口的净增长率为:
![]()
计算近两个世纪来美国人口每年的净增长率,并作出净增长率的散点图,在命令窗口编写MATLAB代码如下:

运行后得到输出结果如图1.3.4所示。
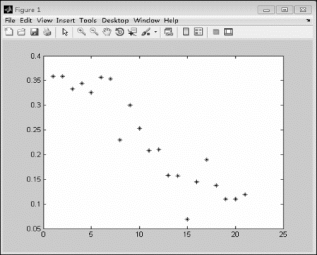
图1.3.4 美国人口净增长率的散点图
观察上述图形可以看出,净增长率并不是常数,但Malthus模型中假设净增长率为常数,因此Malthus模型不能用来预测该数据下的长期人口数量。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




