微分方程解析解示例及MATLAB代码及图示

MATLAB软件中利用命令dsolve（）求微分方程解析解，具体调用格式为：

【语法】

s＝dsolve（′eqn′，′var′）返回微分方程的通解s，参数eqn为微分方程表示式，var为自变量（可省略），默认情况下为变量t；

s＝dsolve（′eqn′，′初始条件1，初始条件2，…，初始条件n′，′var′）返回微分方程的特解s，初始条件1用y（a）＝b表示，初始条件2用Dy（a）＝b表示，依次类推；

［x，y］＝dsolve（′eq1′，′eq2′）返回微分方程组的通解x，y；

［x，y］＝dsolve（′eq1′，′eq2′，′初始条件1′，′初始条件2′）返回微分方程组的特解x，y。

注　用字符串eqn表示方程，D表示导数，D2表示二阶导数，依次类推。

【示例1.2.1】求一阶微分方程y′＝4y－3的通解。

在命令窗口编写MATLAB代码如下：

运行后得到输出结果为：

根据上述结果可知，方程的通解为：

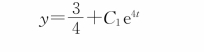
其中，C1为任意常数。

注　当自变量缺省时，默认变量为t，且每次运行中所得到的任意常数表示会有所不同，希望读者注意。

【示例1.2.2】求二阶微分方程y″－6y′＋5y＝0的通解。

在命令窗口编写MATLAB代码如下：

运行后得到输出结果为：

根据上述结果可知，方程的通解为：

其中，C1、C2为通解中的任意常数。

【示例1.2.3】求微分方程y′＝2xy满足初始条件y（0）＝1的特解。

在命令窗口编写MATLAB代码如下：

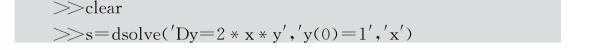
运行后得到输出结果为：

(www.xing528.com)

根据上述结果可知，方程的特解为：

【示例1.2.4】求二阶微分方程y″＝cos x－y满足初始条件y（0）＝1，y′（0）＝－1的特解。

在命令窗口编写MATLAB代码如下：

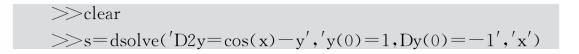
运行后得到输出结果为：

根据上述结果可知，方程的特解为：

【示例1.2.5】求微分方程组的通解。

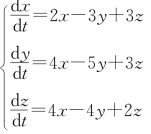
在命令窗口编写MATLAB代码如下：

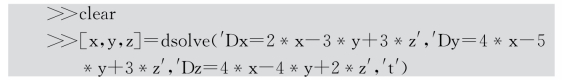
运行后得到输出结果为：

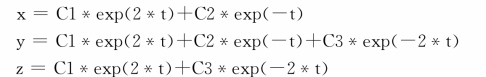
根据上述结果可知，微分方程组的通解为：

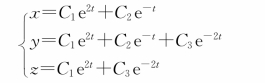
其中，C 1、C 2、C3为通解中的任意常数。

【示例1.2.6】求微分方程xy′＋y－e x＝0满足初始条件y（1）＝2e的特解，并绘制出解的图形。

命令窗口编写MATLAB代码如下：

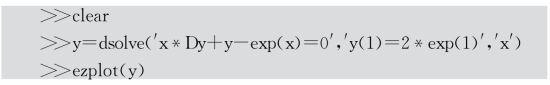
运行后得到输出结果为：

根据上述结果可知，微分方程的特解为：

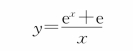
对应解的函数图像如图1.2.1所示。

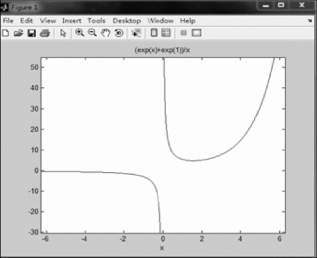
图1.2.1　微分方程的特解