微分方程模型的解主要分为定量解和定性解两大类,定量解通过解析解和数值解对模型结果进行分析,定性解通过解的状态和平衡点类型对模型进行稳定性分析,具体分类如图1.1.2所示。
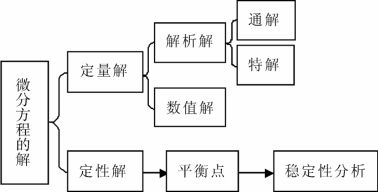
图1.1.2 微分方程解的类型
微分方程的解析解由一个初等函数(特解)或者一族初等函数(通解)构成,而数值解是微分方程的一种近似解,常用的计算数值解方法有欧拉法、龙格-库塔法等;微分方程的稳定性理论主要研究当系统受到各种持续的或者偶然的干扰后,能否保持预定的运行状态,因而稳定性分析在于社会系统、金融系统和生态系统中具有重要的应用价值。
1.解析解
设一阶常微分方程的一般形式为:
![]()
该方程的通解就是寻找一个函数y=f(x),使其满足上述微分方程;如果该函数中含有一个任意常数,则该函数称为微分方程的通解;如果不含任意常数,则该函数称为微分方程的特解。
2.数值解(欧拉法)
设一阶常微分方程的初值问题为:
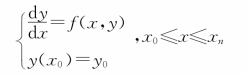
该问题的数值解就是求y(x)在某些等间隔节点x i上的近似值y i来近似y(x i),即y i≈y(x i),i=1,2,…,n。
利用欧拉法求解微分方程模型的数值解就是通过初值递推求解,常用的欧拉递推公式的一般形式为:
![]()
其中,h=x i+1-x i,i=1,2,…,n。
3.平衡点
设一阶自治微分方程(等式右端项不显含自变量x)的一般形式为:(https://www.xing528.com)
![]()
称满足代数方程g(y)=0的实根y=y 0为微分方程的平衡点,也称为奇点或者奇解。方程的平衡点y 0有可能是稳定的,也有可能是不稳定,若g′(y 0)<0,则一阶自治微分方程的平衡点y 0是稳定的;若g′(y 0)>0,则平衡点y 0是不稳定的。
注 二阶自治微分方程的平衡点及其稳定性可做类似的分析。
【示例1.1.4】讨论一阶自治微分方程
![]()
的平衡点及其稳定性。
解 记g(y)=-r(y-1),令g(y)=0,则方程的平衡点为y=1;又因为g′(y)=-r,则g′(1)=-r;
所以当r>0时,平衡点y=1稳定;当r<0时,平衡点y=1不稳定。
【能力训练1.1】
1.已知曲线y=f(x)上任一点处的切线斜率为x 2,且曲线经过点(1,3),试确定该曲线的方程。(提示:利用导数的几何意义建立微分方程模型)
2.将某物体放置于空气中,在时刻t=0时,测得它的温度为u 0=150℃,10分钟后测得温度为u 1=100℃。假设空气的温度保持在ua=24℃,试确定此物体的温度u和时间t的关系,并计算20分钟后物体的温度。(提示:根据Newton冷却定律建立微分方程模型)
3.设A到B城市有条长为30km的高速公路,某天公路上距A城市x km处的汽车密度(每千米多少辆车计)为:
![]()
试计算该高速公路上的汽车总数。(提示:在[x,x+d x]路段上,利用微元法建立微分方程模型计算车辆数)
4.讨论下列一阶自治微分方程的平衡点及稳定性:
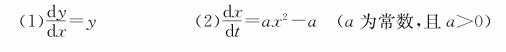
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




